Biết n là số nguyên dương thỏa mãn x n = a 0 + a 1 x - 2 + a 2 x - 2 2 + . . . + a n x - 2 2 và a 1 + a 2 + a 3 = 2 n - 3 . 192 . Mệnh đề nào sau đây đúng?
A. n ∈ 9 ; 16
B. n ∈ 8 ; 12
C. n ∈ 7 ; 9
D. n ∈ 5 ; 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

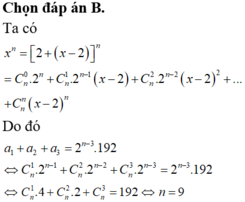

Chọn B
Cách giải: Ta có:
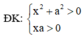
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
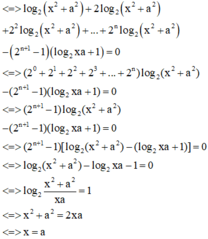
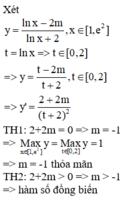
![]()
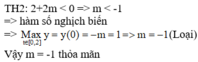

a) ko có a, b thỏa mãn
b) Giá trị lớn nhất của A = \(\frac{7}{6}\)
c) 16
d) x = \(\frac{14}{3}\)
e) x=-1
g) n= 7
h)
j) x=1
k) n=11

a.Vì x,y là số nguyên dương
=> 1003 và 2y cũng là số nguyên dương
Vì 2008 là số chẵn
mà 2y cũng là số chẵn
=> 1003x là số chẵn
Vì 1003 là số lẻ
mà 1003x là số chẵn
=> x là số chẵn
=> x chia hết cho 2 (đpcm)
Vậy ta có đpcm

Bài 1:
Vì trong 3 số nguyên a, b, c có 1 số dương, 1 số âm và 1 số = 0
Ta xét đẳng thức: \(\left|a\right|=b^2.\left(b-c\right)\)(1)
=> a, b, c là số nguyên khác nhau
Nếu a = 0 thì => |a| = 0
=> Đẳng thức (1) trỏ thành: \(b^2.\left(b-c\right)=0\)
Mặt khác:
Do b khác c nên
b2 = 0 => b = 0
=> a = b = 0 (ko thỏa mãn đk.)
Nếu b = 0 thì đẳng thức (1) trở thành:
|a| = 0 . (0 - c)
|a| = 0 (ko thỏa mãn (a khác b))
Nếu c = 0 thì đẳng thức (1) trở thành:
|a| = b2 . b
|a| = b3
Do vì |a| > 0 (a khác 0)
=> b3 > 0
=> b > 0 (3 số lẻ)
=> a < 0
=> a là số dương, b là số âm, c là số 0
Bài 2:
\(n^2-3n^2-36< 0\)
\(\Leftrightarrow-2n^2-36< 0\)
\(\Leftrightarrow-2n^2< 36\)
\(\Leftrightarrow n^2>-18\)
\(\Rightarrow n^2-3n^2-36< 0\)với mọi số tự nhiên
2/ \(A=\frac{\left(1-x\right)^4}{-x}\)
a) Nếu A là số dương
=> \(\frac{\left(1-x\right)^4}{-x}>0\)
=> \(\hept{\begin{cases}\left(1-x\right)^4>0\\-x>0\end{cases}}\)=> x < 0
Vậy nếu x < 0 thì A > 0
b) Nếu A là số âm
=> \(\frac{\left(1-x\right)^4}{-x}< 0\)
=> \(\orbr{\begin{cases}\left(1-x\right)^4< 0\left(1\right)\\-x< 0\left(2\right)\end{cases}}\)
Mà \(\left(1-x\right)^4\ge0\) với mọi giá trị của x
=> Không xảy ra (1) => -x < 0 => x > 0
Vậy nếu x > 0 thì A < 0.
c) Nếu A = 0
=> \(\frac{\left(1-x\right)^4}{-x}=0\)
=> (1 - x)4 = 0
=> 1 - x = 0
=> x = 1
Vậy nếu x = 1 thì A = 0.