Tứ giác ABCD có ∠ B = ∠ A + 10 ° , ∠ C = ∠ B + 10 ° , ∠ D = ∠ C + 10 ° . Khẳng định nào dưới đây là đúng?
A. ∠ A = 65 °
B. ∠ B = 85 °
C. ∠ C = 100 °
D. ∠ D = 90 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ứ giác ABCD có :
ˆB=ˆA+10B^=A^+10(1)(1)
ˆC=ˆB+10C^=B^+10
Thay (1) vào ( 2) ⇒ˆC−10=ˆA+10⇒ˆC=200+ˆA⇒C^−10=A^+10⇒C^=200+A^(2)
ˆD=ˆC+10=200+A+10=300+AD^=C^+10=200+A+10=300+A(3)
(1),(2),(3) =>A+B+C+D=360=>ˆA+10+ˆA+20+ˆA+30+ˆA=360=>4ˆA+60=360=>ˆA=750A+B+C+D=360=>A^+10+A^+20+A^+30+A^=360=>4A^+60=360=>A^=750
=>ˆB=85.;ˆC=950;ˆD=1050=>B^=85.;C^=950;D^=1050.


Theo đề bài : A^=B^+10*
B^=C^+10*
C^=D^+10*
<=> A^- 10* =C^ +10*
B^- 10* = D^ + 10*
Mà A^+B^+C^+D^=360*
=> A^ - 10*+C^ +10* <=> B^ (+10*-10*)+D^+10*+10*
=>2(A^-10*+C^+10*)=360*
=>A^-10*+C^+10*=180*
Ta có : A^-10*=C^+10* =>A^=C^+10*+10*
=> A^=(180*+10*+10*):2=100*
=>C^=180*-100*=80*
=>B^=80*+10*=90*
=>D^=360*-100*-90*-80*=90*
Vậy ....

Tổng bốn góc của 1 tứ giác bằng 360 ° nên: ∠A + ∠ B + ∠ C + ∠ D = 360 °
Suy ra: ∠ A + ∠ B = 360 ° – ( ∠ C + ∠ D) hay
∠ A + ∠ B = 360 ° - 60 ° + 80 ° = 220 °
Mà ∠ A - ∠ B = 10 °
Vậy
∠
A = 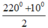 =
115
°
,
∠
B =
115
°
-
10
°
=
105
°
=
115
°
,
∠
B =
115
°
-
10
°
=
105
°

Gọi số đo góc D là xo thì \(\widehat{C}=\left(x+10\right)^o;\widehat{B}=\left(x+20\right)^o;\widehat{A}=\left(x+30\right)^o\)
Do tổng các góc trong tứ giác bằng 360o nên ta có phương trình:
x + x + 10 + x + 20 + x + 30 = 360
\(\Rightarrow x=75\)
Vậy \(\widehat{D}=75^o,\) từ đó suy ra các góc còn lại.

a) Theo bài ra, ta có:
\(\widehat{A}\):\(\widehat{B}\): \(\widehat{C}\) : \(\widehat{D}\) = 1 : 2 : 3 : 4 => \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\widehat{\frac{D}{4}}\) và \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=180^0\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{\widehat{A}}{1}=\widehat{\frac{B}{2}}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)
=> \(\frac{\widehat{A}}{1}=36^0\) => \(\widehat{A}=36^0\)
\(\widehat{\frac{B}{2}}=36^0\)=> \(\widehat{B}=72^0\)
\(\widehat{\frac{C}{3}}=36^0\) => \(\widehat{C}=108^0\)
\(\widehat{\frac{D}{4}}=36^0\) => \(\widehat{D}=144^0\)
Vậy ...
b) Xét tứ giác ABCD có góc A + góc B + góc C + góc D = 3600
hay góc A + (góc A + 100) + góc C + (góc C + 100) = 3600
=> 2.(góc A + góc C) = 3400
=> góc A + góc C = 1700 => góc B + góc D = 3600 - 1700 = 1900
Ta có: góc B = góc A + 100 (1)
góc C = góc B + 100 (2)
góc D = góc C + 100 (3)
Từ (1) và (2) cộng vế cho vế :
góc B + góc C = góc A + 100 + góc B + 100
=> góc C = góc A + 200 => góc C - A = 200
Mà góc A + góc C = 1700
=> 2. góc C = 1900 => góc C = 950
=> góc A = 950 - 200 = 750
Từ (2) và (3) cộng vế cho vế :
góc C + góc D = góc B + 100 + góc C + 100
=> góc D = góc B + 200 => góc D - góc B = 200
Mà góc D + góc B = 1900
=> 2. góc D = 2100 => góc D = 1050
=> góc B = 1050 - 200 = 850
c) Xét tứ giác ABCD góc A + góc B + góc C + góc D = 3600
=> góc A + góc B = 3600 - góc C - góc D = 3600 - 600 - 800 = 2200
Mà góc A - góc B = 100
=> 2. góc A = 2300 => góc A = 1150
=> góc B = 115 - 100 = 1050
Vậy ...

(bài này ko cần vẽ hình bạn nhé ^^!)
a) Tứ giác ABCD có: A^ + B^ +C^ +D^= 360o
A^ + D^ +180o = 360o
A^ +D^ = 180o
b) \(A=\frac{1}{5}D\)
\(\Rightarrow A+D=180o\)
\(\Leftrightarrow\frac{1}{5}D+D=180o\)
\(\frac{6}{5}D=180o\)
\(D=150o\)
\(\Rightarrow A=\frac{1}{5}D=\frac{1}{5}\cdot150o=30o\)
B^ - C^ = 10o => B^ = 10o + C^
=> B^ + C^ = 180o
<=> 10o + 2*C^ = 180o
2C^ = 170o
C^ = 85o
=> B^ = 10o + C^ = 10o + 85o = 95o
Vậy a) A^ + D^ = 180o
b) A^ = 30o
B^ = 95o
C^ = 85o
D^ = 150o
Chọn B
Mà ∠ B = ∠ A + 10 ° (2)
nên từ (1) và (2) => ∠ C - 10 ° = ∠ A + 10 ° => ∠ C = ∠ A + 20 °
Ta có: ∠ D = ∠ C + 10 ° => ∠ D = ∠ A + 20 ° + 10 ° => ∠ D = ∠ A + 30 °
Ta có : ∠ A+ ∠ B+ ∠ C+ ∠ D = 360 ° ( tổng bốn góc của tứ giác)
=> ∠ A+ ∠ A + 10 ° + ∠ A + 20 ° + ∠ A + 30 ° = 360 °
=> 4 ∠ A + 60 ° = 360 °
Do đó: ∠ A= 75 °
=> ∠ B = ∠ A + 75 ° + 10 ° = 85 °
=> ∠ C= ∠ A+ 20 ° = 95 °
=> ∠ D= ∠ A+ 30 ° = 105 °