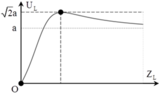
Đặt vào hai đầu đoạn mạch RLC một điện áp xoay chiều u = U 0 cos ( ω t ) V , thay đổi L thì thấy điện áp hiệu dụng hai đầu đoạn mạch chứa L có dạng như hình vẽ. Tỉ số giữa Z C và R là:
A. 1.
B. 2.
C. 0,5.
D. 0,25.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ đồ thị ta thấy Z L = 100 Ω v à Z L = ∞ là hai giá trị của Z L cho cùng điện áp hiệu dụng U trên đoạn mạch chứ L.
Ta có
1 Z L 1 + 1 Z L 2 = 2 Z L 0 → Z L 2 = ∞ Z L 0 = R 2 + Z C 2 Z C = 2 Z L 1 = 2 .100 Ω .
Mặc khác Z L = 100 Ω cũng là giá trị để điện áp hiệu dụng trên điện trở cực đại → Z L = Z C = 100 Ω .
Từ hai kết quả trên ta tìm được R = 100 Ω
Đáp án A

Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa .
U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03
Đáp án C

Từ đồ thị ta xác định được khi 2 U = U Z L Z L − Z C ⇒ Z L = 2 Z C .
Đáp án B

Từ đồ thị ta thấy Z C = 100 Ω tổng trở cực tiểu (mạch xảy ra cộng hưởng) Z = R = 100 Z C = Z L = 100 .
Mặc khác khi Z C → ∞ thì U C = U = 200 V .
Từ hai kết quả trên ta tìm được U C m a x = U R 2 + Z L 2 R = 200 2 V .
Đáp án D

Từ đồ thị ta xác định được U = 220 ⇒ U 0 = U 2 = 220 2 V .
Đáp án D

Từ đồ thị, ta thấy rằng ω R = 2 ω C → n = 4.
Áp dụng công thức chuẩn hóa U L m a x = U 1 − n − 2 ⇒ U L m a x U = 1 1 − n − 2 = 1 , 03 .
Đáp án C

Từ đồ thị ta xác định được a = U Z L Z L = U ⇒ U 0 = 2 a V .
Đáp án B

Từ đồ thị ta xác định được Z C = 120 Ω v à Z C = 525 Ω là hai giá trị của Z C cho cùng một điện áp hiệu dụng trên tụ.
Ta có 1 Z C 1 + 1 Z C 2 = 2 Z C 0 ⇒ Z C 0 ≈ 195 Ω .
Đáp án A
Từ đồ thị ta xác định được U L m a x = U R R 2 + Z C 2 = 2 a U = a ⇒ Z C = R
Đáp án A