Gọi S = (a; b) là tập tất cả các giá trị của tham số thực m để phương trình
log 2 ( m x - 6 x 3 ) + log 1 2 ( - 14 x 2 + 29 x - 2 ) = 0 có 3 nghiệm phân biệt. Khi đó hiệu H = b-a bằng
A. 5 2
B. 1 2
C. 2 3
D. 5 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Kiến thức bổ sung: Dạng toán tìm GTLN, GTNN của hàm số y = |u(x)| trên đoạn [a;b]
Gọi M, m lần lượt là GTLN, GTNN của hàm số u(x) trên đoạn [a;b]
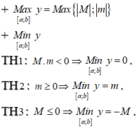
Đặt: ![]()
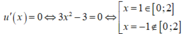
Ta có: ![]()
Suy ra: ![]()
![]()
TH1: ![]()
![]() (loại)
(loại)
(vì ko thỏa mãn giả thiết Aa = 12)
TH2: ![]()
![]()
Từ giả thiết: Aa = 12 ![]()
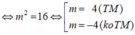
TH3: ![]()
![]()
Từ giả thiết: Aa = 12 ![]()
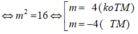
Kết hợp các trường hợp suy ra: S = {-4;4}
Vậy tổng các phần tử của bằng: (-4) + 4 = 0.

a) Xét ΔAEM vuông tại A và ΔDCM vuông tại D có
\(\widehat{AME}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔAEM\(\sim\)ΔDCM(g-g)
b) Xét ΔBAC vuông tại A và ΔBDE vuông tại D có
\(\widehat{B}\) chung
Do đó: ΔBAC\(\sim\)ΔBDE(g-g)
Suy ra: \(\dfrac{BA}{BD}=\dfrac{BC}{BE}\)
hay \(BA\cdot BE=BD\cdot BC\)
c) Ta có: ΔAEM\(\sim\)ΔDCM(cmt)
nên \(\dfrac{MA}{MD}=\dfrac{ME}{MC}\)
hay \(\dfrac{MA}{ME}=\dfrac{MD}{MC}\)
Xét ΔMAD và ΔMEC có
\(\dfrac{MA}{ME}=\dfrac{MD}{MC}\)
\(\widehat{AMD}=\widehat{EMC}\)(hai góc đối đỉnh)
Do đó: ΔMAD\(\sim\)ΔMEC(c-g-c)
Suy ra: \(\widehat{MAD}=\widehat{MEC}\)

a) Vì \({13^2} - 24.13 + 143 = 0\) nên \(x = 13\) là nghiệm của phương trình \( \Rightarrow 13 \in S\)
Vậy mệnh đề “\(13 \in S\)” đúng.
b) Vì \({11^2} - 24.11 + 143 = 0\) nên \(x = 11\) là nghiệm của phương trình \( \Rightarrow 11 \in S\)
Vậy mệnh đề “\(11 \notin S\)” sai.
c) Ta có:
\(\begin{array}{l}{x^2} - 24x + 143 = 0\\ \Leftrightarrow {x^2} - 11x - 13x + 11.13 = 0\\ \Leftrightarrow x.\left( {x - 11} \right) - 13.\left( {x - 11} \right) = 0\\ \Leftrightarrow \left( {x - 11} \right).\left( {x - 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 13\end{array} \right.\end{array}\)
Tập nghiệm của phương trình là \(S=\{11;13\}\)
Phương trình có 2 nghiệm hay \(n\;(S) = 2\)
=> Mệnh đề “\(n\;(S) = 2\)” đúng.

a: Sửa đề; CM AN/AM=AB/AC
AN/AM=AH^2/AC:AH^2/AB=AB/AC
b: Tham khảo:

Tham khảo hình vẽ:
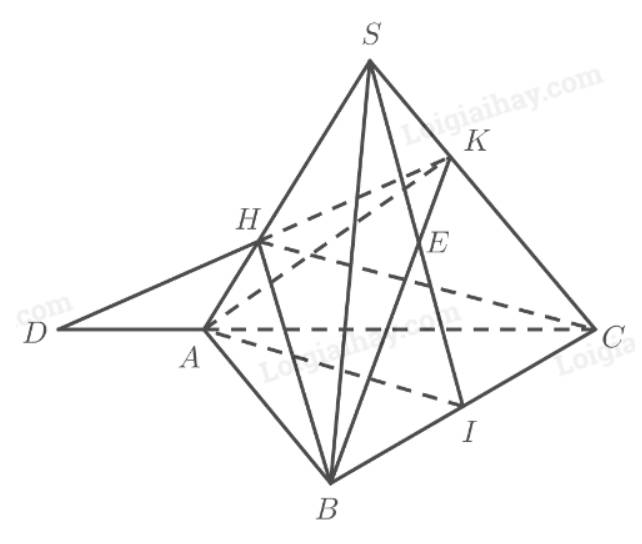
a) Gọi \(D = HK \cap AC\). Ta có:
\(\left. \begin{array}{l}D \in AC \subset \left( {ABC} \right)\\D \in HK\end{array} \right\} \Rightarrow M = HK \cap \left( {ABC} \right)\)
b) Gọi \(E = SI \cap BK\). Ta có:
\(\left. \begin{array}{l}E \in SI \subset \left( {SAI} \right)\\E \in BK \subset \left( {ABK} \right)\end{array} \right\} \Rightarrow E \in \left( {SAI} \right) \cap \left( {ABK} \right)\)
Mà \(A \in \left( {SAI} \right) \cap \left( {ABK} \right)\).
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {ABK} \right)\) là đường thẳng \(AE\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in \left( {SAI} \right)\\I \in BC \subset \left( {BCH} \right)\end{array} \right\} \Rightarrow I \in \left( {SAI} \right) \cap \left( {BCH} \right)\\\left. \begin{array}{l}H \in SA \subset \left( {SAI} \right)\\H \in \left( {BCH} \right)\end{array} \right\} \Rightarrow H \in \left( {SAI} \right) \cap \left( {BCH} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {SAI} \right)\) và \(\left( {BCH} \right)\) là đường thẳng \(HI\).