Tìm tập các giá trị thực của tham số m để phương trình 4 ( 2 + 1 ) x + 2 - 1 x - m = 0 có đúng hai nghiệm âm phân biệt.
A. (2;4)
B. (3;5)
C. (4;5)
D. (5;6)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2

Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
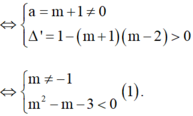
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
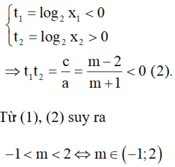

Đáp án B.
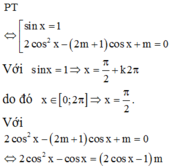
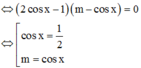
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
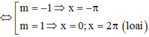
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
![]()
Vậy m= -1; m=0.

Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt  , tìm điều kiện của t.
, tìm điều kiện của t.
Đưa về bất phương trình dạng ![]()
Cách giải :
![]()

Ta có 

Đặt  , khi đó phương trình trở thành
, khi đó phương trình trở thành
![]()

![]()
![]()
![]()
![]()
Ta có: 



Vậy 