Tìm x là số nguyên để mỗi phân số sau nhận giá trị nguyên 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để phân số này là số nguyên thì \(2x-5\in\left\{1;-1;19;-19\right\}\)
hay \(x\in\left\{3;2;12;-7\right\}\)

\(C\in Z\Leftrightarrow\left\{{}\begin{matrix}\dfrac{n-2}{2n+3}\in Z\left(1\right)\\\dfrac{n^2+2n+4}{2n+3}\in Z\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow n-2⋮2n+3\\ \Leftrightarrow2n-4⋮2n+3\\ \Leftrightarrow2n+3\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ \Leftrightarrow n\in\left\{-5;-2;-1;2\right\}\left(3\right)\\ \left(2\right)\Leftrightarrow2n^2+4n+8⋮2n+3\\ \Leftrightarrow2n\left(n+3\right)-\left(2n+3\right)+11⋮2n+3\\ \Leftrightarrow2n+3\inƯ\left(11\right)=\left\{-11;-1;1;11\right\}\\ \Leftrightarrow n\in\left\{-7;-2;-1;4\right\}\left(4\right)\\ \left(3\right)\left(4\right)\Leftrightarrow n\in\left\{-2;-1\right\}\)
Vậy ...

a) Để phân số \(\dfrac{26}{x+3}\) nguyên thì \(26⋮x+3\)
\(\Leftrightarrow x+3\in\left\{1;-1;2;-2;13;-13;26;-26\right\}\)
hay \(x\in\left\{-2-4;-1;-5;10;-16;23;-29\right\}\)
b) Để phân số \(\dfrac{x+6}{x+1}\) nguyên thì \(x+6⋮x+1\)
\(\Leftrightarrow5⋮x+1\)
\(\Leftrightarrow x+1\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{0;-2;4;-6\right\}\)
c) Để phân số \(\dfrac{x-2}{x+3}\) nguyên thì \(x-2⋮x+3\)
\(\Leftrightarrow-5⋮x+3\)
\(\Leftrightarrow x+3\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{-2;-4;2;-8\right\}\)
d) Để phân số \(\dfrac{2x+1}{x-3}\) nguyên thì \(2x+1⋮x-3\)
\(\Leftrightarrow7⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;7;-7\right\}\)
hay \(x\in\left\{4;2;10;-4\right\}\)

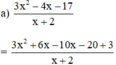
(Tách -4x = 6x – 10x để nhóm với 3x2 xuất hiện x + 2)
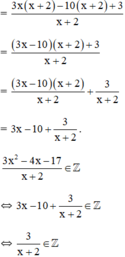
⇔ x + 2 ∈ Ư(3) = {±1; ±3}
+ x + 2 = 1 ⇔ x = -1
+ x + 2 = -1 ⇔ x = -3
+ x + 2 = 3 ⇔ x = 1
+ x + 2 = -3 ⇔ x = -5
Vậy với x = ±1 ; x = -3 hoặc x = -5 thì phân thức có giá trị nguyên.
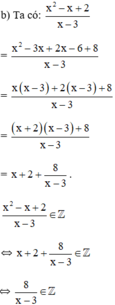
⇔ x – 3 ∈ Ư(8) = {±1; ±2; ±4; ±8}
+ x – 3 = 1 ⇔ x = 4
+ x – 3 = -1 ⇔ x = 2
+ x – 3 = 2 ⇔ x = 5
+ x – 3 = -2 ⇔ x = 1
+ x – 3 = 4 ⇔ x = 7
+ x – 3 = -4 ⇔ x = -1
+ x – 3 = 8 ⇔ x = 11
+ x – 3 = -8 ⇔ x = -5.
Vậy với x ∈ {-5; -1; 1; 2; 4; 5; 7; 11} thì giá trị phân thức là số nguyên.

Ta có:\(\dfrac{x-2}{x+3}=\dfrac{x+3-5}{x+3}=1-\dfrac{5}{x+3}\)
Để bt có giá trị là số tự nhiên thì \(5⋮x+3\Rightarrow x+3\inƯ_{\left(5\right)}=\left\{\pm1;\pm5\right\}\)
| x + 3 | 1 | -1 | 5 | -5 |
| x | -2 | -4 | 2 | -8 |
| Kết luận | thỏa mãn | loại | thỏa mãn | loại |
=> \(x=\pm2\)
Giải:
a) \(\dfrac{x-2}{x+3}\)
Để \(\dfrac{x-2}{x+3}\) là số tự nhiên thì \(x-2⋮x+3\)
\(x-2⋮x+3\)
\(\Rightarrow x+3-5⋮x+3\)
\(\Rightarrow5⋮x+3\)
\(\Rightarrow x+3\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Ta có bảng giá trị:
| x+3 | -5 | -1 | 1 | 5 |
| x | -8 | -4 | -2 | 2 |
Ta thấy:
Nếu \(x\in\left\{-8;-4;2\right\}\) thì \(\dfrac{x-2}{x+3}\) sẽ là số tự nhiên
Vậy \(x\in\left\{-8;-4;2\right\}\)
Chúc bạn học tốt!

`( 3x + 2 )/( x + 2 )` nguyên `.`
`=> 3x + 2` \(\vdots\) `x+2`
`=> 3x + 6 - 4` \(\vdots\) `x+2`
`=> 3( x + 2 )-4` \(\vdots\) `x+2`
Do `3( x + 2 )` \(\vdots\) `x+2` mà để `3( x + 2 )-4` \(\vdots\) `x+2`
`=> -4` \(\vdots \) `x+2` hay `x+2 in Ư_(4) = { +-1 ; +-2 ; +-4 }`
Do `x in ZZ^-`
`=> x + 2 in ZZ` `; x + 2 < 2`
`=> x + 2 in { +-1 ; -2 ; -4 }`
`=> x in { -1 ; -3 ; -4 ; -6 }`
Vậy `x in { -1;-3;-4;-6}`

a) Để A là phân số thì : \(n-2\ne0=>n\ne2\)
b) Để A nhận giá trị nguyên âm lớn nhất
\(=>A=-1\\ =>\dfrac{n-6}{n-2}=-1\\ =>n-6=-\left(n-2\right)\\ =>n-6=-n+2\\ =>n+n=6+2\\ =>2n=8\\ =>n=4\left(TMDK\right)\)
c) \(A=\dfrac{n-6}{n-2}=\dfrac{n-2-4}{n-2}=1-\dfrac{4}{n-2}\)
Để A nhận gt số nguyên thì : \(\dfrac{4}{n-2}\in Z=>4⋮\left(n-2\right)\\ =>n-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\\ =>n\in\left\{3;1;4;0;6;-2\right\}\)
Đến đây bạn lập bảng giá trị rồi thay từng gt n vào bt A, giá trị nào cho A là STN thì bạn nhận gt đó ạ.
d) Mình nghĩ bạn thiếu đề ạ

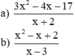
\(\Rightarrow\dfrac{3x^2-6x+5x-10+14}{x-2}=3x+5+\dfrac{14}{x-2}\in Z\\ \Rightarrow x-2\inƯ\left(14\right)=\left\{-14;-7;-2;-1;1;2;7;14\right\}\\ \Rightarrow x\in\left\{-12;-5;0;1;3;4;9;16\right\}\)
Để phân số này là số nguyên thì \(x-2\in\left\{1;-1;2;-2;7;-7;14;-14\right\}\)
hay \(x\in\left\{3;1;4;0;9;-5;16;-12\right\}\)