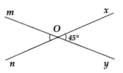
Cho góc xOy có số đo bằng 45°.Vẽ hai tia Om, On lần lượt là tia đối của tia Oy, Ox. Tính số đo các góc còn lại trên hình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
13 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
18 tháng 10 2021
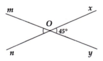
Vì Om, On đối Oy, Ox nên \(\widehat{xOy}=\widehat{mOn}=45^0\left(đối.đỉnh\right)\)
Ta có \(\widehat{xOy}+\widehat{xOm}=180^0\left(kề.bù\right)\Rightarrow\widehat{xOm}=180^0-45^0=135^0\)
Vì Om, On đối Oy, Ox nên \(\widehat{xOm}=\widehat{yOn}=135^0\left(đối.đỉnh\right)\)
TN
18 tháng 10 2021
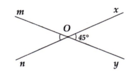
ta có : mOn=xOy=45o
Do xOy và xOm kề bù nên:
xOy+xOm=180o
suy ra:xOm=180o - xOy=135o
Mà yOn và xOm đối đỉnh nên
yOn=xOm=135o
19 tháng 9 2023
`#3107`
`1,`
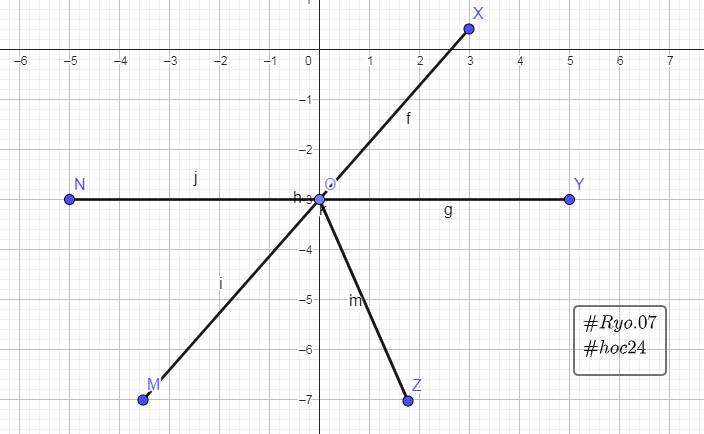
`a)` Yc là tính \(\widehat{yOm}\) và \(\widehat{xOn}\) phải k c? Ba điểm x, O, m cùng nằm trên 1 đt' mà?
Vì \(\widehat{xOy}\) và \(\widehat{xOn}\) là 2 góc kề bù
\(\widehat{xOy} + \widehat{xOn} = 180^0 \\ \Rightarrow 50^0 + \widehat{xOn} = 180^0 \\ \Rightarrow \widehat{xOn} = 130^0\)
Vì \(\widehat{xOn}\) và \(\widehat{yOm}\) là 2 góc đối đỉnh
`=>`$ \widehat{xOn} = \widehat{yOm} = 130^0$
Vậy, $ \widehat{xOn} = \widehat{yOm} = 130^0.$
`b)`
Vì Oz là tia phân giác của $\widehat{yOm}$
`=>` $\widehat{mOz} = \widehat{yOz} = \dfrac{1}{2} \widehat{yOm}$
`=>` $\widehat{mOz} = \dfrac{1}{2} . 130^0 = 65^0$
Vậy, $\widehat{mOz} = 65^0.$
CC
29 tháng 7 2019
yOz kề bù với xOy
=> yOz + xOy = 180o
=> yOz = 150o
Ot là p/g của xOy => xOt = tOy = xOy/2 = 15o
Om là p/g của yOz => zOm = yOm = yOz/2 = 75o
Vì yOz kề bù với xOy
=> Tia Ox,Oz đối nhau
=> zOm và xOm kề bù
=> zOm + xOm = 180o => xOm = 105o
Vì xOt < xOm ( 15o<105o)
=> Ot nằm giữa Ox, Om
=> xOt + tOm = xOm
=> tOm = 90o
Có xOn + xOm = 105o +75o = 180o
=> xOn và xOm kề bù
=> Om, On đối nhau
3 tháng 5 2017
Bạn thông cảm, mình chưa biết vẽ hình trên máy tính nên mình chỉ ghi chữ thôi nhé
a) vì Ox,Oy,Oz cùng thuộc một nửa mặt phẳng bờ là tia Ox và góc xOy < góc xOz (30°<120°) nên tia Oy nằm giữa hai tia Ox và Oz
b) vì tia Oy nằm giữa hai tia Ox và Oz nên:
xOy+yoz=xOz
Thay số vào ta có: 30°+yOz=120°
yOz=120°_30°= 90°
c) vì Om là tia phân giác của xOy nên Om nằm giữa Ox và Oy
và xOm=mOy=xoy/2=30°/2=15°
Vì On là tia phân giác của yOz nên On nằm giữa Oy và Oz
và yOn=nOz=yOz/2=120°/2=60°
Vì tia Oy nằm giữa hai tia Ox và Oz
Tia Om nằm giữa hai tia Ox và Oy
Tia On nằm giữa hai tia Oy và Oz thì tia Oy nằm giữa hai tia Om và On nên
mOy+yOn=mOn
Thay số vào ta có:15°+60°=mOn
15°+60°=75°
Vậy mOn=75°
26 tháng 3 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOz}\left(40^0< 120^0\right)\)
nên tia Oy nằm giữa hai tia Ox và Oz
\(\Leftrightarrow\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\)
\(\Leftrightarrow\widehat{yOz}+40^0=120^0\)
hay \(\widehat{yOz}=80^0\)
Vậy: \(\widehat{yOz}=80^0\)
KV
1 tháng 12 2023
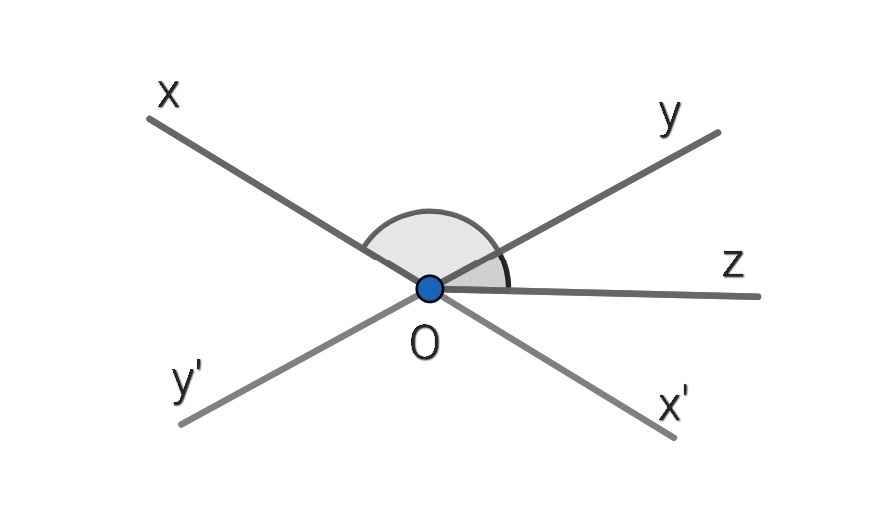a) Ta có:
∠xOy + ∠yOz = 150⁰
∠xOy - ∠yOz = 90⁰
⇒ ∠xOy = (150⁰ + 90⁰) : 2 = 120⁰
⇒ ∠yOz = 120⁰ - 90⁰ = 30⁰
b) Ta có:
∠xOy + ∠x'Oy = 180⁰ (kề bù)
⇒ ∠x'Oy = 180⁰ - ∠xOy
= 180⁰ - 120⁰
= 60⁰