Biết rằng parabol
y
=
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
=
1
thành hai phần có diện tích lần lượt là
S
1
,
S
2
với
S
1
<
S
2
. Tỉ số
S
1
S
2
bằng ...
Đọc tiếp
Biết rằng parabol
y
=
1
24
x
2
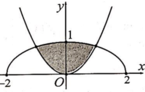
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
=
1
thành hai
phần có diện tích lần lượt là
S
1
,
S
2
với
S
1
<
S
2
. Tỉ số
S
1
S
2
bằng
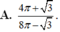
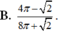
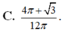
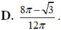
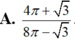
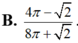
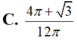
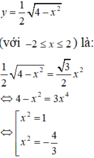
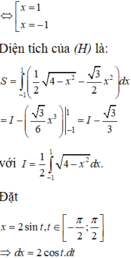
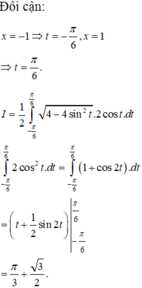
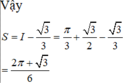
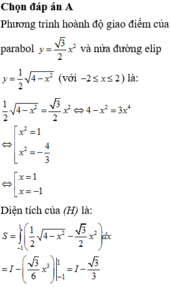
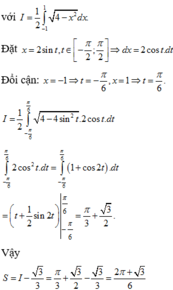
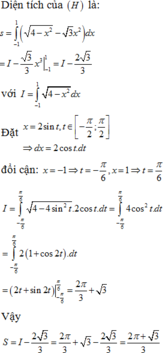
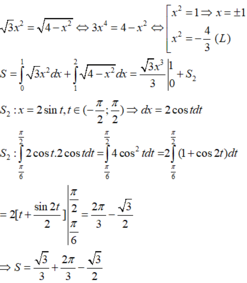
Đáp án A
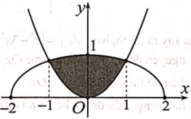
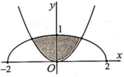
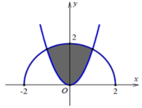
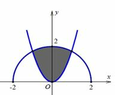
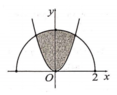
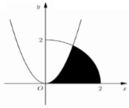
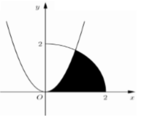
Nhận thấy S 1 là diện tích hình phẳng giới hạn bởi parabol y = 1 24 x 2 và phần elip nằm phía trên trục hoành.
Ta có phương trình hoành độ giao điểm của parabol y = 1 24 x 2 và elip x 2 16 + y 2 1 = 1 là