Mặt cầu đi qua tất cả các đỉnh của một hình lập phương cạnh a có bán kính bằng
A. 2 a 2
B. 3 a 4
C. 3 a 2
D. 6 a 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



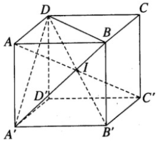
Tâm là giao điểm các đường chéo (O)
Bán kính mặt cầu là OA = 1/2 AC’
Đường chéo hình vuông cạnh a là a√2 (AC = a√2)
Xét tam giác vuông ACC’ tại C:
⇒ bán kính mặt cầu đi qua 8 đỉnh hình lập phương là (a√3)/2

Gọi I là tâm của hình lập phương. Tất cả các đỉnh của hình lập phương đều có khoảng cách đến I bằng 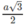 nên chúng nằm trên mặt cầu tâm I bán kính
nên chúng nằm trên mặt cầu tâm I bán kính 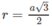
Ta có diện tích mặt cầu đó là S = 4 πr 2 = 3 πa 2

ý B nha
Nếu cái này ở bài 2 vòng 19 luyện thi lp 5 thì đúng 1000000000000000000000000000% đó.....

Phương pháp:
Xác định tâm đường tròn ngoại tiếp O, O ' của hai tam giác đáy. Khi đó, tâm mặt cầu ngoại tiếp hình lăng trụ là trung điểm của OO’.
Cách giải:
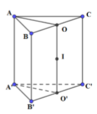
Do tam giác ABC vuông cân tại A nên trung điểm O của BC là tâm đường tròn ngoại tiếp tam giác ABC.
Tương tự, trung điểm O’ của B’C’ là tâm đường tròn ngoại tiếp tam giác A’B’C’.
Khi đó, tâm mặt cầu I ngoại tiếp hình lăng trụ là trung điểm của OO’.


Chọn A
Cách 1:
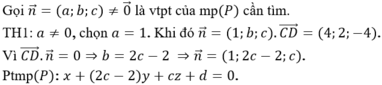

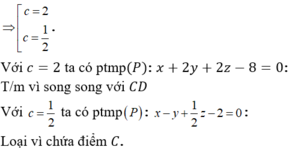

Cách 2: Ta có  nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
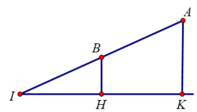
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
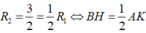
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà ![]() nên ta có 2a + b - 2c = 0 => b = 2c - 2a
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
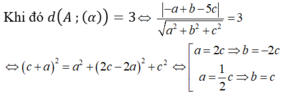
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0

Chọn A.
Phương pháp:
Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp có cạnh bên vuông góc với đáy là
R = h 2 4 + S d a y 2
trong đó h là chiều cao của khối chóp và Rday là bán kính đường ròn ngoại tiếp đáy.
Cách giải:

