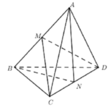
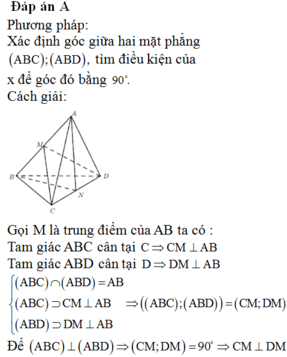
Cho tứ diện ABCD có (ACD) ⊥ (BCD) và AC=AD=BC=a.Với giá trị nào của x thì (ABC) ⊥ (ABD)?
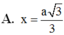
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

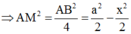

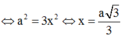

Đáp án A
Phương pháp:
Xác định góc giữa hai mặt phẳng (ABC); (ABD), tìm điều kiện của x để góc đó bằng 900
Cách giải:
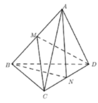
Gọi M là trung điểm của AB ta có :
Tam giác ABC cân tại C => CM ⊥ AB
Tam giác ABD cân tại D => DM ⊥ AB
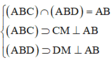
![]()
Để ![]()
![]() vuông tại M
vuông tại M
Gọi N là trung điểm của CD, chứng minh tương tự như trên ta có:
![]()
Xét tam giác vuông ANC có:
![]()
![]()
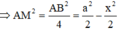
Xét tam giác vuông ACM có: 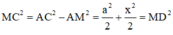
Để ∆CDM vuông tại M ![]()
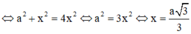

Phương pháp:
Xác định góc giữa hai mặt phẳng ![]()
- Tìm giao tuyến ![]()
- Xác định 1 mặt phẳng ![]()
- Tìm các giao tuyến ![]()
- Góc giữa hai mặt phẳng ![]()
Cách giải:
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là các tam giác cân tại A, B
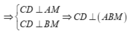
và ![]()
Dễ dàng chứng minh được ![]()
![]() tại I
tại I
suy ra ![]()
![]()
![]()
Lại có: ![]()
![]()
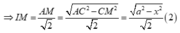
Từ (1), (2) suy ra: 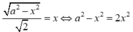
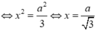
Chọn: B

Đáp án A
Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc ⇒ V A B C D = A B . A C . A D 6
Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc ⇒ V M . N P Q = M N . M P . M Q 6
Ta chứng minh được M N A B + M P A C + M Q A D = 1 ( dựa vào định lý Thalet), khi đó
M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27
Vậy V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27

Gọi I, J, K lần lượt là trung điểm của BD, CD, BC.
Thể tích khối tứ diện vuông ABCD là:
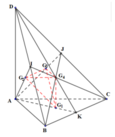
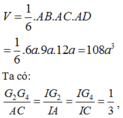
tương tự:
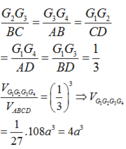
Chọn: A