Cho hình chóp S.ABCD có đáy là ABCD là hình chữ nhật với A B = 2 a , B C = a 3 . Điểm H là trung điểm của cạnh AB, SH là đường cao, góc giữa SD và đáy là 60 o . Khi đó thể tích khối chóp là?
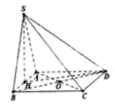
A. a 3 3 6
B. 2 a 3
C. 4 a 3
D. a 3 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc đề là \(SM=a\sqrt{3}\) vì không có điểm H nào trong dữ liệu
\(BC=AD=\sqrt{BD^2-AB^2}=a\sqrt{2}\)
a.
Qua M kẻ đường thẳng song song BC cắt CD tại E
\(\Rightarrow CD\perp ME\Rightarrow CD\perp\left(SME\right)\)
\(\Rightarrow\widehat{SEM}\) là góc giữa (SCD) và (ABCD)
Áp dụng định lý talet trong tam giác BCD:
\(\dfrac{EM}{BC}=\dfrac{DM}{BD}=\dfrac{3}{4}\Rightarrow EM=\dfrac{3}{4}BC=\dfrac{3a\sqrt{2}}{4}\)
\(\Rightarrow tan\widehat{SEM}=\dfrac{SM}{EM}=\dfrac{2\sqrt{6}}{3}\)
\(\Rightarrow\widehat{SEM}\approx58^031'\)
b.
\(BC||AD\Rightarrow BC||\left(SAD\right)\)
\(\Rightarrow d\left(BC;AD\right)=d\left(BC;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Lại có: BM cắt (SAD) tại D, mà \(BD=\dfrac{4}{3}MD\)
\(\Rightarrow d\left(B;\left(SAD\right)\right)=\dfrac{4}{3}d\left(M;\left(SAD\right)\right)\)
Trong mp (ABCD), từ M kẻ \(MH\perp AD\)
Trong mp (SMH), từ M kẻ \(MK\perp SH\)
\(\Rightarrow MK\perp\left(SAD\right)\Rightarrow MK=d\left(M;\left(SAD\right)\right)\)
Talet cho tam giác ABD:
\(\dfrac{MH}{AB}=\dfrac{MD}{BD}=\dfrac{3}{4}\Rightarrow MH=\dfrac{3}{4}AB=\dfrac{3a}{4}\)
Hệ thức lượng trong tam giác vuông SMH:
\(MK=\dfrac{SM.MH}{\sqrt{SM^2+MH^2}}=\dfrac{3a\sqrt{19}}{19}\)
\(\Rightarrow d\left(SD;BC\right)=\dfrac{4}{3}MK=\dfrac{4\sqrt{19}}{19}\)

Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
![]()
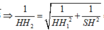
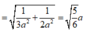
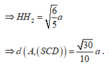
=> Chọn phương án B.

Đáp án B
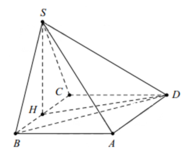
Tam giác HCD vuông tại C ⇒ H D = H C 2 + C D 2 = a 6 2
Tam giác BCD vuông tại C ⇒ sin C B D ⏜ = C D B D = 1 3
Suy ra bán kính đường tròn ngoại tiếp Δ H B D là
R Δ H B D = H D 2. sin H B D ⏜ = a 6 2 : 2 3 = 3 a 2 4
Bán kính mặt cầu cần tính là R = R Δ H B D 2 + S H 2 4 = a 5 2
Đáp án: C
Hướng dẫn giải:
Ta có: H D = H A 2 + A D 2 = 2 a
Ta có: S A B C D = A B . B C = 2 a 2 3
⇒ V S . A B C D = 1 3 S H . S A B C D = 4 a 3