Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ đỉnh B đến mặt phẳng (ACD).
A . a 6 2
B . a 3 2
C . a 6 3
D . a 2 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 6 2019
Đáp án C
Khoảng cách từ B bằng với chiều cao của tứ diện đều ABCD. Do đó ta dễ dàng suy ra được: d B , A C D = a 6 3 .
Chọn phương án C.
CM
24 tháng 5 2019
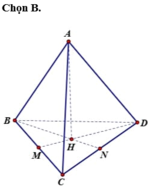
Gọi hình chiếu vuông góc hạ từ A đến mặt phẳng (BCD) là H. Khoảng cách từ A đến mặt phẳng (BCD) là AH.
Vì tứ diện đều nên H là trọng tâm tam giác BCD
CM
6 tháng 9 2017
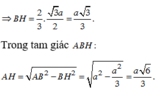
Chọn B.
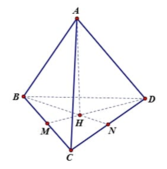
Gọi hình chiếu vuông góc hạ từ A đến mặt phẳng (BCD) là H. Khoảng cách từ A đến mặt phẳng (BCD) là AH.
Vì tứ diện đều nên H là trọng tâm tam giác BCD
⇒ B H = 2 3 . 3 a 2 = a 3 3
Trong tam giác ABH
A H = A B 2 - B H 2 = a 2 - a 2 3 = a 6 3
CM
12 tháng 10 2019
Chọn C
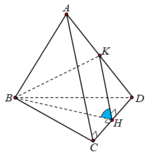
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
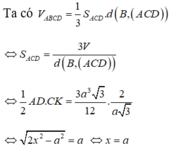
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
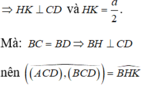
Mặt khác:
Tam giác ABD có:
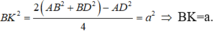
Tam giác BHK có:
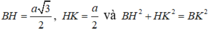
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
CM
28 tháng 8 2019
Đáp án B
Gọi O là tâm của tam giác BCD và M là trung điểm CD
⇒
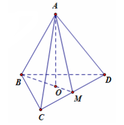A
O
⊥
(
B
C
D
)
⇒
d
A
;
B
C
D
=
A
O
=
6
Đặt độ dài cạnh của tứ diện ABCD là x ⇒ B O = 2 B M 3 = x 3 3
⇒ A O = A B 2 - B O 2 = x 6 3 = 6 ⇔ x = 3 6
⇒ V = S B C D . A O 3 = x 2 3 . A O 12 = 27 3
CM
27 tháng 5 2017
Đáp án C
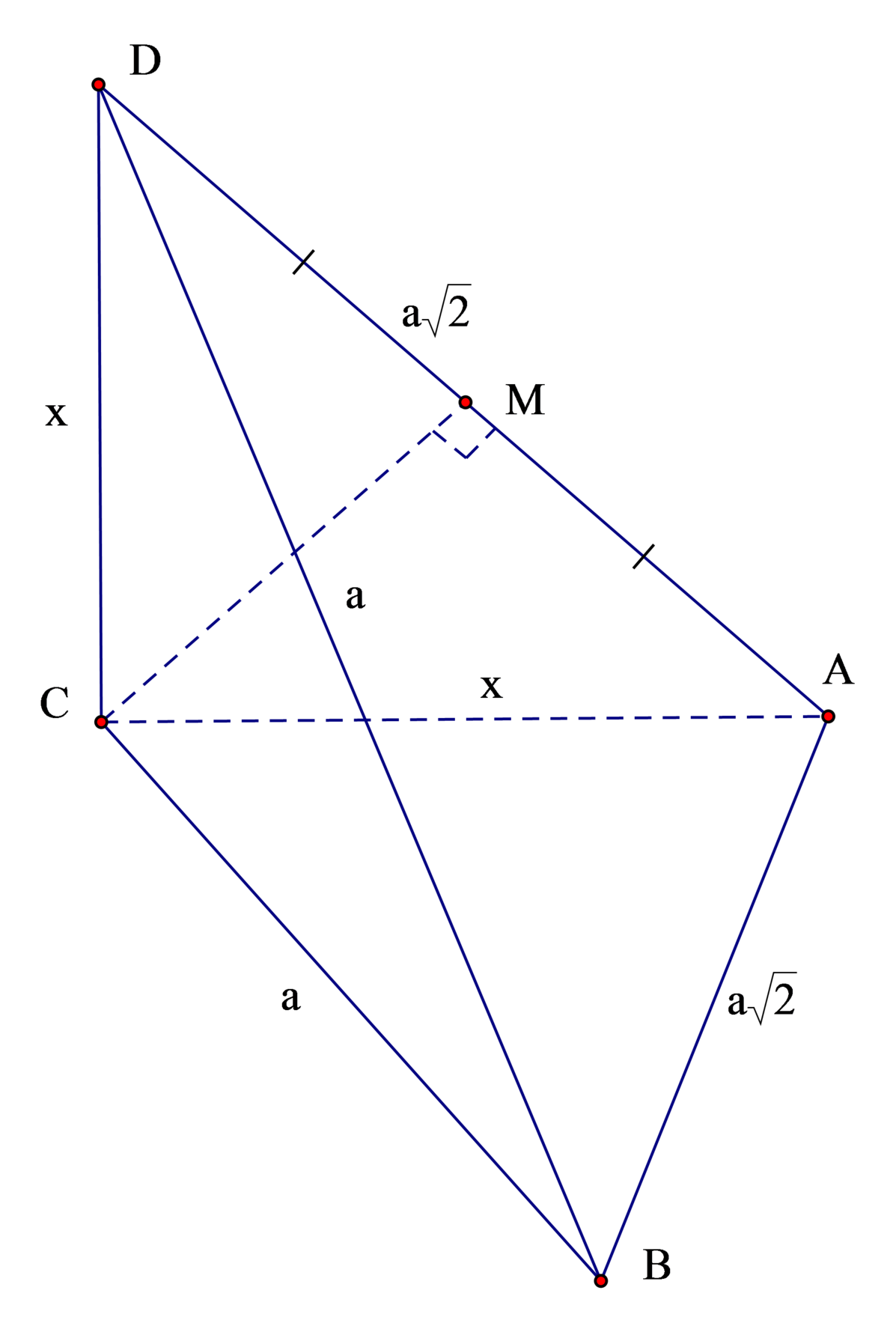
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0
Đáp án C
Khoảng cách từ B bằng với chiều cao của tứ diện đều ABCD. Do đó ta dễ dàng suy ra được:
=> Chọn phương án C.