Cho hình nón tròn xoay có đường cao là a 3 , đường kính đáy là 2a. Tìm diện tích xung quanh của hình nón đã cho.
A . 2 3 πa 2
B . 2 πa 2
C . πa 2
D . 4 3 πa 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
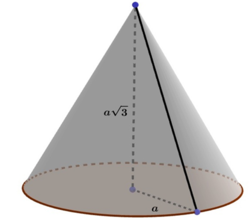
Dễ có chu vi của đáy là hình tròn bằng: p = π d = 2 π a
Khoảng cách từ đỉnh đến một điểm thuộc vành của hình nón bằng: . S A = S H 2 + H A 2 = 3 a 2 + a 2 = 2 a
Suy ra diện tích xung quanh hình nón là diện tích hình quạt có bán kính 2a và độ dài cung là 2 π a . Ta dễ tính được chu vi của hình tròn bán kinh 2a là 4 π a . Do đó diện tích hình quạt cần tính bằng nửa hình tròn này. Từ đây ta thu được kết quả: S x q = 2 π a 2 .
Chọn đáp án B.

Phương pháp:
Công thức tính diện tích xung quanh hình nón có bán kính đáy R, chiều cao h và đường sinh l:


a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
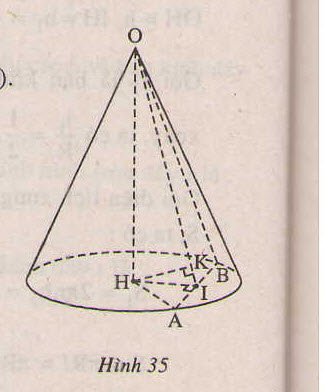

Đáp án A
Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a 2 và góc giữa đường sinh và mặt phẳng đáy là SAO ^ = 60°.

Đáp án B
Dễ có chu vi của đáy là hình tròn bằng: p = π d = 2 π a
Khoảng cách từ đỉnh đến một điểm thuộc vành của hình nón bằng:
SA =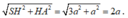
Suy ra diện tích xung quanh hình nón là diện tích hình quạt có bán kính 2a và độ dài cung là 2 π a. Ta dễ tính được chu vi của hình tròn bán kinh 2a là 4 π a. Do đó diện tích hình quạt cần tính bằng nửa hình tròn này. Từ đây ta thu được kết quả: S x q = 2 πa 2 => Chọn đáp án B.