Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Gọi ∆ là đường thẳng cần tìm
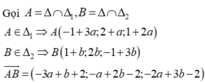
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
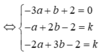
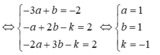
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương 
Vậy phương trình của ∆ là
Chọn A.
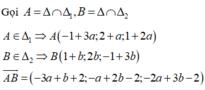
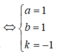
Ta có A(2;3;3); B(2;2;2)
Δ đi qua điểm A(2;3;3) và có vectơ chỉ phương A B → = 0 ; - 1 ; 1
Vậy phương trình của ∆ là x = 2 y = 3 - t z = 3 - t
Chọn C.
*) Gọi A = d1 ∩ (α)
A ∈ d1 ⇒ A(2-a;1+3a;1+2a)
Mà điểm A thuộc mp(α) nên thay tọa độ điểm A vào phương trình mặt phẳng ta được
(2 - a) + 2(1 + 3a) – 3(1 + 2a) – 2= 0
2 – a + 2 + 6a – 3 – 6a – 2 = 0
⇒ a = -1 ⇒ A(3;-2;-1)
*) Gọi B = d2 ∩ (α)
B ∈ d2 ⇒ B(1-3b;-2+b;-1-b)
Mà điểm B thuộc mp(α) nên thay tọa độ điểm B vào phương trình mặt phẳng ta được:
(1 - 3b) + 2(-2 + b) - 3(-1 - b) - 2 = 0
1- 3b – 4 + 2b + 3 + 3b - 2 = 0
⇔ 2b - 2 = 0 ⇔ b = 1 ⇒ B(-2;-1;-2)
*) Đường thẳng d đi qua điểm A(3;-2;-1) và có vectơ chỉ phương 
Vậy phương trình chính tắc của d là x - 3 - 5 = y + 2 1 = z + 1 - 1
Chọn B
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).
Chọn A
Mặt phẳng qua I vuông góc với d có phương trình
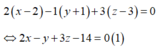
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào (1) ta có
Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
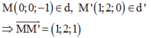
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
Phương trình mặt phẳng
Đáp án C
Gọi tâm mặt cầu cần tìm là I và H,K lần lượt là hình chiếu của I lên các đường thẳng d 1 , d 2 .
Ta có: I H + I K ≥ H K ≥ a d 1 , d 2 . Dấu bằng khi HK là đường vuông góc chung của d 1 , d 2 và I là trung điểm của HK.
Khi đó: H 2 a , a , 4 và K 3 − b , b , 0 ⇒ K H ¯ 2 a + b − 3 ; a − b ; 4
Đường thẳng d 1 , d 2 có vecto chỉ phương lần lượt là u 1 ¯ = 2 ; 1 ; 0 và u 2 ¯ − 1 ; 1 ; 0 nên:
K H ¯ . u 1 ¯ = 0 K H ¯ . u 2 ¯ = 0 ⇔ 2 2 a + b − 3 + a − b + 0.4 = 0 − 2 a + b − 3 + a − b + 0.4 = 0 ⇔ 2 a + b − 3 = a − b = 0 ⇔ a = b = 1
Suy ra trung điểm của HK là I 2 ; 1 ; 2 và bán kính của mặt cầu (S) là R = H K 2 = 2.