Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A. Phát biểu không đúng : Nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua tỉ lệ thuận với cường độ dòng điện, với điện trở của dây dẫn và với thời gian dòng điện chạy qua
Nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua tỷ lệ thuận với bình phương cường độ dòng điện, với điện trở của dây dẫn và thời gian dòng điện chạy qua.
Hệ thức: Q = I 2 .R.t (trong đó: I là cường độ dòng điện (A), R là điện trở dây dẫn (Q), t là thời gian dòng điện chạy qua (s), Q là nhiệt ìượng tỏa ra (J)).
Mặt khác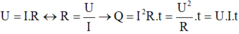
ta có:
do I tỉ lệ nghịch với điện trở nên I=2I'=0,1A
do U tỉ lệ thuận với cường độ dòng điện nên I'''=3I=0,6A
Ta có: \(\dfrac{I}{I'}=\dfrac{\dfrac{U}{R}}{\dfrac{U}{R'}}=\dfrac{R'}{R}=\dfrac{2R}{R}=2\Rightarrow I'=\dfrac{I}{2}=\dfrac{0,2}{2}=0,1\left(A\right)\)
Ta có: \(\dfrac{I}{I"}=\dfrac{U}{U"}=\dfrac{U}{3U}=\dfrac{1}{3}\Rightarrow I'=\dfrac{I}{\dfrac{1}{3}}=\dfrac{0,2}{\dfrac{1}{3}}=0,6\left(A\right)\)
Chọn D. Điện trở R tỉ lệ thuận với hiệu điện thế U và tỉ lệ nghịch với cường độ dòng điện I chạy qua đoạn mạch
Cường độ dòng điện: \(I=\dfrac{U}{R}\)
\(I'=\dfrac{U}{R'}\)
Suy ra: \(\dfrac{I}{I'}=\dfrac{R'}{R}=2\)
\(\Rightarrow I'=\dfrac{I}{2}=0,3A\)
Q = I2.R.t và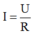 
⇒ Nhiệt lượng Q còn được tính bởi công thức khác: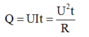 
→ Đáp án A
Ta có: Q = I 2 R t
Lại có: I = U R
=> Nhiệt lượng Q còn được tính bởi các công thức khác: Q = U I t = U 2 R t
Đáp án: A
\(\Rightarrow\left\{{}\begin{matrix}I=\dfrac{U}{R}\\I'=\dfrac{U}{3R}\\I-I'=0,6A\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}I=3I'\\3I'-I'=0,6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}I=3.0,3=0,9A\\I'=0,3A\end{matrix}\right.\)\(\Rightarrow I=0,9A\)
D
Q=RI2t => Nhiệt lượng toả ra tỉe lệ với I2