Hàm số y = x 4 + 8 x 3 + 5 đồng biến trên khoảng nào sau đây?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

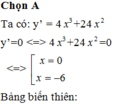


Đáp án B
Phương pháp:
Hàm số y = f(x) đồng biến (nghịch biến) trên (a;b) khi và chỉ khi ![]() và f’(x) = 0tại hữu hạn điểm.
và f’(x) = 0tại hữu hạn điểm.
Cách giải:
Quan sát bảng biến thiên, ta thấy: hàm số y = f(x) đồng biến trên khoảng (0;2). Do ![]() Hàm số y = f(x) đồng biến trên khoảng (0;1)
Hàm số y = f(x) đồng biến trên khoảng (0;1)

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Chọn D.
Nhận xét: Từ đồ thị f'(x) , ta có 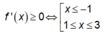
Từ đó 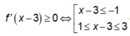
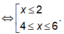
Do đó chọn D.

Chọn đáp án B.
Dựa vào bảng biến thiên hàm số đồng biến trên khoảng (0;1)