Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, S A = a . Gọi α là góc giữa hai mặt phẳng S B C và A B C bằng
A. 3
B. 1 2
C. 2
D. 1 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Lời giải.
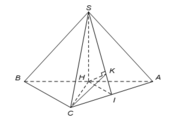
Ta có
![]()
![]()
![]()
Từ (1) và (2)
![]()
Gọi I là trung điểm AC
![]()
Mặt khác
![]()
Từ (3) và (4)
![]()
![]()
![]()
![]()
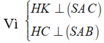
nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC.
Xét tam giác CHK vuông tại K, có
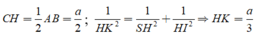
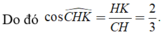
Đáp án C
Dựng A E ⊥ B C .
Lại có S A ⊥ A B S A ⊥ A C ⇒ S A ⊥ B C
Do đó B C ⊥ S E A ⇒ S B C ; A B C ⏜ = S E A ⏜
Mặt khác:
A E = B C 2 = a 2 2 ⇒ tan α = t a n S E A ⏜ = S A A E = 2