Với a ≥ 0 và b ≥ 0, chứng minh a + b 2 ≥ a + b 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
18 tháng 9 2023
Lời giải:
Từ $a+b> c\Rightarrow a+b-c>0$ (cái này hiển nhiên)
Từ $|a-b|< c\Leftrightarrow |a-b|^2< c^2$
$\Leftrightarrow (a-b)^2< c^2$
$\Leftrightarrow (a-b-c)(a-b+c)<0$
Với $c>0$ thì $a-b-c< a-b+c$ nên để tích âm thì $a-b-c<0< a-b+c$
Hay $a-b-c<0$ và $a-b+c>0$
CM
28 tháng 5 2018
a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .
29 tháng 5 2016
Đề bài : Cho \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\left(a,b,c\ne0\right)\)và \(M=\frac{b^2c^2}{a}+\frac{c^2a^2}{b}+\frac{a^2b^2}{c}\)
Chứng minh M=3abc.
Trước tiên, ta chứng minh bài toán phụ : Cho x+y+z=0 . Chứng minh \(x^3+y^3+z^3=3xyz\)
Giải bài toán phụ như sau : Ta có : \(x+y+z=0\Rightarrow z=-\left(x+y\right)\Rightarrow z^3=-\left[x^3+y^3+3xy\left(x+y\right)\right]\)
\(\Rightarrow x^3+y^3+z^3=-3xy\left(x+y\right)=-3xy\left(-z\right)\)
\(\Rightarrow x^3+y^3+z^3=3xyz\)
Áp dụng vào bài đã cho, ta suy ra : \(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)
Do đó : \(M=\frac{b^2c^2}{a}+\frac{c^2a^2}{b}+\frac{a^2b^2}{c}=\frac{a^2b^2c^2}{a^3}+\frac{a^2b^2c^2}{b^3}+\frac{a^2b^2c^2}{c^3}=a^2b^2c^2\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)=a^2b^2c^2.\frac{3}{abc}=3abc\)Vậy \(M=3abc\)(đpcm)
4 tháng 6 2021
Áp dụng bđt bunhiacopxki có:
\(\left(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\right)\left(x+y+z\right)\ge\left(a+b+c\right)^2\)
\(\Leftrightarrow\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}\)
Dấu "=" xảy ra <=> \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)
AT
5 tháng 6 2021
BĐT này gọi là BĐT Cauchy-Schwarz đó bạn.
Chứng minh BĐT: \(\dfrac{a^2}{x}+\dfrac{b^2}{y}\ge\dfrac{\left(a+b\right)^2}{x+y}\)
\(\Rightarrow\dfrac{a^2y+b^2x}{xy}\ge\dfrac{\left(a+b\right)^2}{x+y}\Rightarrow\left(a^2y+b^2x\right)\left(x+y\right)\ge\left(a+b\right)^2.xy\)
\(\Leftrightarrow a^2y^2+b^2x^2-2abxy\ge0\Leftrightarrow\left(ay-by\right)^2\ge0\) (luôn đúng)
Áp dụng BĐT trên vào đề:
Ta được: \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b\right)^2}{x+y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}\)
AT
0
NV
4 tháng 4 2023
\(P=\dfrac{4}{a^2+b^2}+\dfrac{1}{ab}=\dfrac{4}{\left(a+b\right)^2-2ab}+\dfrac{1}{ab}=\dfrac{4}{2-2ab}+\dfrac{1}{ab}=\dfrac{2}{1-ab}+\dfrac{1}{ab}\)Áp dụng BĐT Bunhiacopxki dạng phân thức ta có:
\(\dfrac{2}{1-ab}+\dfrac{1}{ab}\ge\dfrac{\left(\sqrt{2}+1\right)^2}{1-ab+ab}=\left(\sqrt{2}+1\right)^2\) hay \(P\ge\left(\sqrt{2}+1\right)^2\)
Dấu "=" xảy ra khi \(\dfrac{\sqrt{2}}{1-ab}=\dfrac{1}{ab};a+b=\sqrt{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=\sqrt{2}\\ab=\dfrac{1}{\sqrt{2}+1}\end{matrix}\right.\Leftrightarrow\left(a;b\right)=\left(1;-1+\sqrt{2}\right),\left(-1+\sqrt{2};1\right)\)
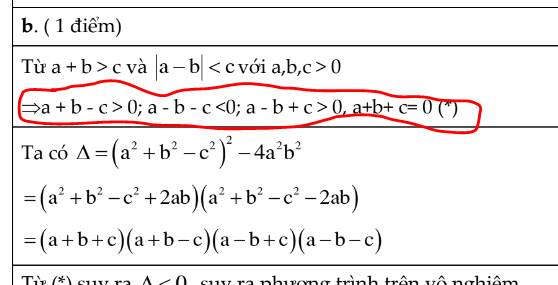
Vì a ≥ 0 nên a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇒ a - 2 a b + b ≥ 0 ⇒ a + b ≥ 2 a b
⇒ a + b + a + b ≥ a + b + 2 a b
⇒ 2(a + b) ≥ a 2 + 2 a b + b 2