Trên mặt phẳng tọa độ Oxyz, cho các điểm A(1;0;3), B(2;3;-4), C(-3;1;2). Xét điểm D sao cho ABCD là hình bình hành. Khi đó tọa độ của D là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Hình chiếu của A(1 ;2 ;3) lên trục Ox là M(1;0;0)
Hình chiếu của A(1 ;2 ;3) lên trục Oy là N(0;2;0)
Hình chiếu của A(1 ;2 ;3) lên trục Ox là P(0;0;3)
Phương trình mặt phẳng (P) cần tìm là:
![]()

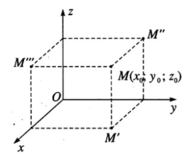
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )

Đáp án B
Phương pháp:
Hình chiếu của điểm M(x0;y0;z0) trên trục Ox là điểm M1(x0;0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oy là điểm M2(0;y0;0)
Hình chiếu của điểm M(x0;y0;z0) trên trục Oz là điểm M3(0;0;z0)
Phương trình theo đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c), (a,b,c ≠ 0) là: x a + y b + z c = 1
Cách giải: Hình chiếu của điểm A(2; –1;1) trên các trục tọa độ Ox, Oy, Oz lần lượt là: (2;0;0), (0; –1;0), (0;0;1)
Phương trình mặt phẳng (α): x 2 + y - 1 + z 1 = 1





Chọn C