Cho tứ diện ABCD, đáy BCD là tam giác vuông tại C, B C = C D = a 3 , góc A B C ^ = A D C ^ = 90 ° , khoảng cách từ B đến (ACD) là a 2 . Khi đó thể tích khối cầu ngoại tiếp ABCD là:
A. 4 π a 3 3 .
B. 12 π a 3 .
C. 12 π a 3 3 .
D. 4 π 3 a 3 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
Chúc bạn học tốt ^^

Đáp án C
Gọi I là trung điểm BC.
Ta có; tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
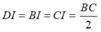 (1)
(1)
Tam giác ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC nên:
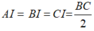 (2)
(2)
Từ (1) và (2) suy ra: 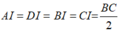
Do đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.

Câu 3.
Tam giác \(ABC\)vuông cân tại \(A\)nên \(\widehat{ACB}=45^o\).
Tam giác \(BCD\)vuông cân tại \(B\)nên \(\widehat{BCD}=45^o\).
\(\widehat{ACD}=\widehat{ACB}+\widehat{BCD}=45^o+45^o=90^o\)
\(\Rightarrow AC\perp CD\)
mà \(AC\perp AB\)
nên \(AB//CD\)
suy ra \(ABCD\)là hình thang vuông.
Câu 4.
Kẻ \(BE\perp CD\)khi đó \(\widehat{BED}=90^o\).
Tứ giác \(ABED\)có \(4\)góc vuông nên là hình chữ nhật, mà \(AB=AD\)nên \(ABED\)là hình vuông.
\(BE=DE=AB=2\left(cm\right)\)
\(EC=CD-DE=4-2=2\left(cm\right)\)
Suy ra tam giác \(BEC\)vuông cân tại \(E\)
Suy ra \(\widehat{EBC}=\widehat{ECB}=45^o\)
\(\widehat{ABC}=\widehat{ABE}+\widehat{EBC}=90^o+45^o=135^o\)
Đáp án A
+ Gọi I là trung điểm AC (do Δ A B C vuông tại B)
⇒ I A = I C = I B = I D ⇒ I là tâm mặt cầu ngoại tiếp ABCD
+ Gọi M là trung điểm của BC => M là tâm đường tròn ngoại tiếp Δ B C D
⇒ I M là trục của đường tròn ngoại tiếp Δ B C D ⇒ I M ⊥ B C D
+ Gọi N, H lần lượt là hình chiếu của M lên CD và I N ⇒ M H ⊥ I C N
⇒ M H = d M ; I C N = d M ; A C D = 1 2 d B ; A C D = a 2 2
+ N là trung điểm của CD ⇒ M N = 1 2 B C = a 3 2
Có 1 I M 2 + 1 M N 2 = 1 M H 2 ⇒ I M 2 = 3 a 2 2
I C 2 = C M 2 + M H 2 = 3 a 2 ⇒ R = I C = a 3
⇒ V = 4 3 π R 3 = 4 3 π a 3 3 = 4 π a 3 3