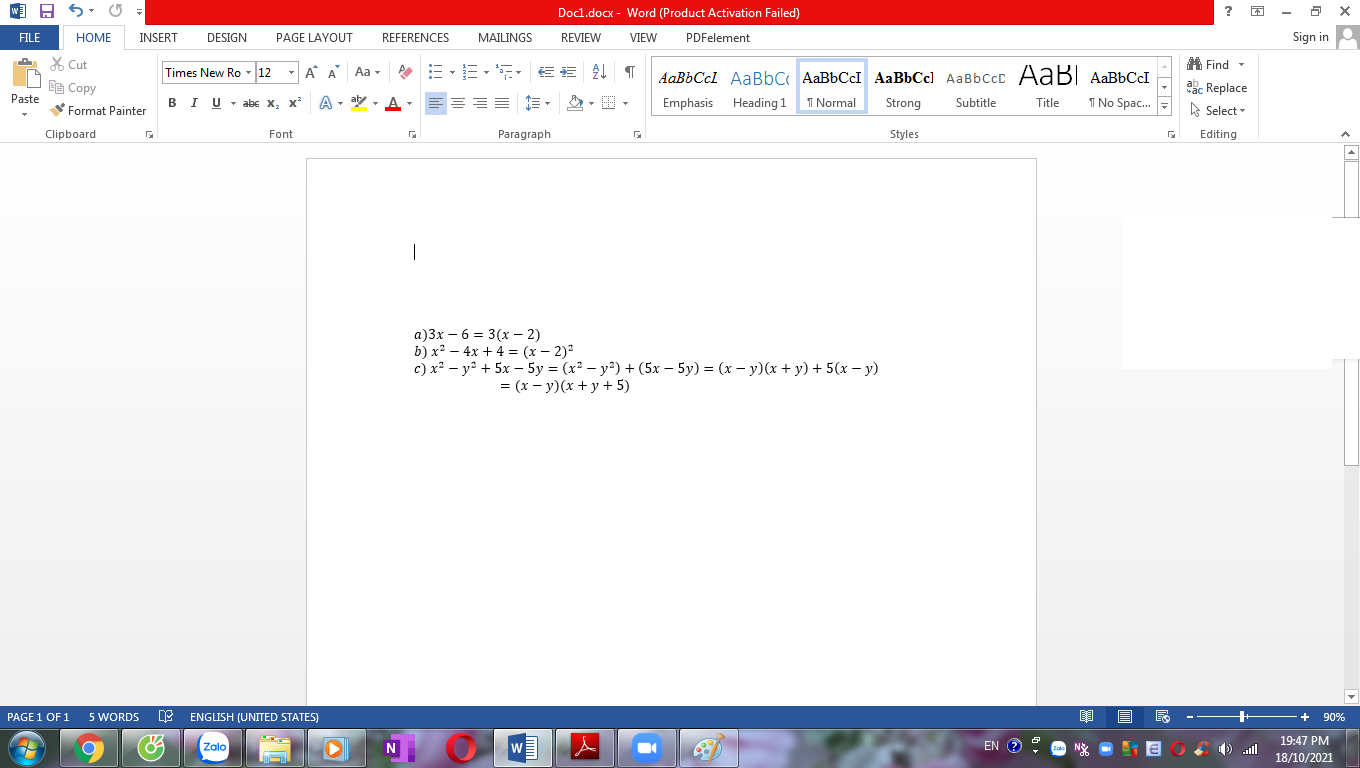
Cộng các phân thức: 4 y - x z - x + 3 y - x y - z + 3 y - z x - z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

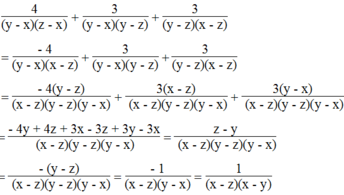

a ) \(\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}\)
= \(\frac{z-x}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{x-y}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\)
= \(\frac{z-x+x-y+y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=0\)
b ) \(\frac{4}{\left(y-x\right)\left(z-x\right)}+\frac{3}{\left(y-x\right)\left(y-z\right)}+\frac{3}{\left(y-z\right)\left(x-z\right)}\)
= \(\frac{-4}{\left(y-x\right)\left(x-z\right)}+\frac{3}{\left(y-x\right)\left(y-z\right)}+\frac{3}{\left(y-z\right)\left(x-z\right)}\)
= \(\frac{-4\left(y-z\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}+\frac{3\left(x-z\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}+\frac{3\left(y-x\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}\)
= \(\frac{-4y+4z+3x-3z+3y-3x}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}=\frac{z-y}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}\)
= \(\frac{-\left(y-x\right)}{\left(x-z\right)\left(y-z\right)\left(y-x\right)}=\frac{-1}{\left(x-z\right)\left(y-z\right)}=\frac{1}{\left(x-z\right)\left(x-y\right)}\)
Chúc bạn học tốt !!!

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.

\(\frac{x}{3}=\frac{y}{4}=\frac{z}{6}=\frac{x+y+z}{3+4+6}=\frac{52}{13}=4\)
\(\Rightarrow\frac{x}{3}=4\Rightarrow x=12\)
\(\frac{y}{4}=4\Rightarrow y=16\)
\(\frac{z}{6}=4\Rightarrow z=24\)

t chỉ cho kết quả thôi nhá, còn nhóm nhân tử you tự xử nhá !
=(x-y)(z-x)(z-y)(x+y+z)
\(\left(x-y\right)z^3+\left(z-z\right)y^3+\left(y-z\right)x^3\)
\(=z^3\left(x-y\right)+y^3\left(z-x\right)+x^3\left(y-z\right)\)
\(=xz^3-yz^3+\left(z-x\right)y^3+\left(y-z\right)x^3\)
\(=xz^3-yz^3+y^3z-xy^3+\left(y-z\right)x^3\)
\(=xz^3-yz^3+y^3z-xy^3+y^3z-xy^3+x^3y-x^3z\)
Mk ko chắc

Do câu d mình ko biết làm bởi v mình không làm được