Cho hình nón tròn xoay có bán kính đáy R, chiều cao h và góc ở đỉnh là góc
α
không là góc nhọn. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác. Khi đó tam giác có diện tích lớn nhất là: A.
1
2
(
h
2
+
R
2
)
B.
1
2
(
h
2
+
R
)
π
C.
...
Đọc tiếp
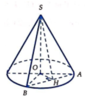
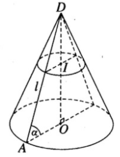
Cho hình nón tròn xoay có bán kính đáy R, chiều cao h và góc ở đỉnh là góc α không là góc nhọn. Một mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác. Khi đó tam giác có diện tích lớn nhất là:
A. 1 2 ( h 2 + R 2 )
B. 1 2 ( h 2 + R ) π
C. 1 2 ( h + R 2 ) h
D. 1 2 ( h 2 - R 2 )
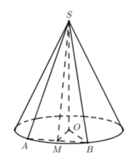
Đáp án A
Giả sử thiết diện là một tam giác cân có độ dài chiều cao hạ từ đỉnh nón xuống đáy tam giác là x ( 0 < x < R 2 + h 2 )
Khi đó ta dễ dàng tính được độ dài đáy tam giác theo x, h và R là:
2 R 2 + h 2 - x 2
Do đó, diện tích S của tam giác là:
Vậy S m a x = R 2 + h 2 2