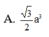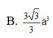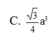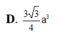Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A có BC = 2a. Biết góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 ∘ và khoảng cách giữa hai đường thẳng A'A, BC bằng a 3 2 . Tính thể tích lăng trụ ABC.A'B'C'