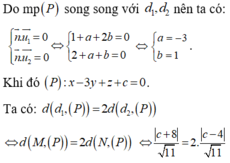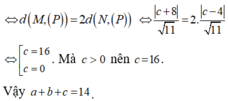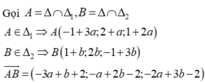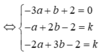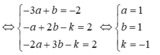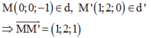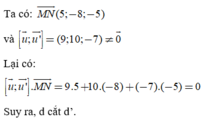Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 1 2
và d 2 : x - 1 2 = y - 1 1 = z + 2 1 . Mặt phẳng (P) : x + ay + bz + c = 0 song song
với d 1 , d 2 và khoảng cách từ d 1 đến (P) bằng 2 lần khoảng cách từ d 2 đến (P).
Giá trị của a + b + c bằng
A. 6
B. 14
C. -4
D. -6