Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng: 2 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 8 2023
4:
a: Gọi độ dài cạnh góc vuông cần tìm là x
Theo đề, ta có: x^2+x^2=a^2
=>2x^2=a^2
=>x^2=a^2/2=2a^2/4
=>\(x=\dfrac{a\sqrt{2}}{2}\)
b:
Độ dài cạnh là;
\(h:\dfrac{\sqrt{3}}{2}=\dfrac{2h}{\sqrt{3}}\)
5:
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>13^2=12^2+HB^2
=>HB=5cm
BC=5+16=21cm
ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>AC^2=16^2+12^2=400
=>AC=20(cm)
TD
2
KK
3 tháng 1 2017
vì tam giác đó là tam giác vuông cân nên 2 cạnh góc vuông bằng nhau
Gọi cạnh huyền của tam giác đó là x
Theo định lý Pytago ta có: x2 = 22 + 22
x2 = 4 + 4
x2 = 8
x = căn 8
mk ko có máy tính nên bạn tự tính nhé
14 tháng 1 2017
Bài này dễ thế mà mi góp ý là những câu hỏi dễ như thế này bạn nên tự suy luận vì kiến thức thầy cô đã dạy hết rồi
1V
1
26 tháng 3 2022
Vì tam giác trên là tam giác vuông cân
=> Cạnh đáy bằng cạnh góc vuông
Áp dụng định lí Py - ta - go ta có :
Cạnh huyền2 = cạnh góc vuông2 + cạnh đáy2 = 22 +22 = 8
=> Cạnh huyền = \(\sqrt{8}\)(cm)
LT
2
25 tháng 7 2018
Vì một cạnh góc vuông = 5cm => cạnh góc vuông kia cũng = 5cm
Theo định lý PTG ta có: 5^2 + 5^2 = cạnh huyền^2
25 + 25 = 50
=> cạnh huyền = \(\sqrt{50}\)(cm)
25 tháng 7 2018
Tam giác vuông cân
=> Hai cạnh góc vuông bằng nhau
Và cùng bằng 5 cm
Độ dài cạnh huyền là: \(\sqrt{5^2+5^2}=5\sqrt{2}\) (cm) (Áp dụng định lý Pytago trong tam giác vuông)
LT
1
30 tháng 7 2018
Gọi tam giác đó vuông cân tại A, 2 góc ở đáy là B và C
Áp dụng định lý Pytago ta có :
BC^2 = AB^2 + AC^2
hay BC^2 = 7^2 + 7^2 = 98
=> BC = \(\sqrt{98}\)
Vậy,...........
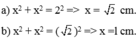
Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)
Áp dụng định lí pitago ta có:
x2 +x2 =(√2)2⇒ 2x2 = 2 => x2 =1
=> x=1cm