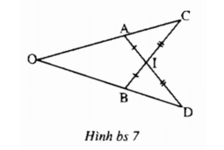
Cho hình bs 7. Chứng minh rằng OA = OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
3
13 tháng 5 2017
Xét tam giác IAC và IBD có:
IA = IB ( theo đề bài)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( theo đề bài )
Do đó: tam giác IAC = tam giác IBD (c.g.c)
Suy ra góc ACI = góc BDI ( 2 góc tương ứng) \(\left(1\right)\)
Suy ra góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = \(180^0\)(2 góc kề bù)
góc OBI + góc IBD = \(180^0\)(2 góc kề bù)
mà: góc IAC = góc IBD (*)
Suy ra góc: OAI = góc OBI (5)
Xét tam giác: OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
Do đó: tam giác OAD = tam giác OBC (g.c.g)
Suy ra: OA = OB (2 cạnh tương ứng)
20 tháng 1 2019
Xét tam giác IAC và tam giác IBD có:
IA = IB ( gt)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( gt )
=> Tam giác IAC = tam giác IBD (c.g.c)
=> Góc ACI = góc BDI ( 2 góc tương ứng) (1)
và góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = 1800 (2 góc kề bù)
góc OBI + góc IBD = 1800 (2 góc kề bù)
mà: góc IAC = góc IBD (*)
=> góc: OAI = góc OBI (5)
Xét tam giác OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
=> Tam giác OAD = tam giác OBC (g.c.g)
=> OA = OB (2 cạnh tương ứng)
23 tháng 11 2023
a: Xét ΔOBD và ΔOAC có
\(\widehat{OBD}=\widehat{OAC}\)
OB=OA
\(\widehat{BOD}\) chung
Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC
OB+BC=OC
OA+AD=OD
mà OB=OA và OC=OD
nên BC=AD
b: Xét ΔADC và ΔBCD có
AD=BC
CD chung
AC=BD
Do đó: ΔADC=ΔBCD
c: ΔADC=ΔBCD
=>\(\widehat{IDC}=\widehat{ICD}\)
=>ΔIDC cân tại I
=>ID=IC
ID+IB=BD
IC+IA=AC
mà ID=IC và BD=AC
nên IB=IA
d: Xét ΔOAI và ΔOBI có
OA=OB
AI=BI
OI chung
Do đó: ΔOAI=ΔOBI
=>\(\widehat{AOI}=\widehat{BOI}\)
=>OI là phân giác của góc AOB
=>OI là phân giác của góc COD
ΔCOD cân tại O
mà OI là đường phân giác
nên OI\(\perp\)CD
CM
24 tháng 5 2017
Xét ΔOAC và ΔOBD có:
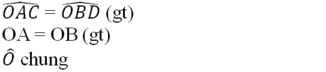
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD (hai cạnh tương ứng).
VT
0
31 tháng 8 2023
a: Xét ΔABD và ΔBAC có
BA chung
AD=BC
BD=AC
Do đó; ΔABD=ΔBAC
=>góc OAB=góc OBA
=>OA=OB
OA+OC=AC
OB+OD=BD
mà OA=OB và AC=BD
nên OC=OD
b: Xét ΔODE vuông tại D và ΔOCE vuông tại C có
OE chung
OD=OC
Do đó; ΔODE=ΔOCE
=>ED=ED
c: Xét ΔADE và ΔBCE có
AD=BC
góc ADE=góc BCE
DE=CE
Do đó: ΔADE=ΔBCE
=>EA=EB
11 tháng 12 2021
a: Xét ΔOAC và ΔODB có
OA=OD
\(\widehat{O}\) chung
OC=OB
Do đó: ΔOAC=ΔODB
YP
21 tháng 10 2021
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
+) Xét ∆AIC và ∆BID có:
AI = BI (giả thiết)
∠AIC = ∠BID ( hai góc đối đỉnh).
IC = ID ( giả thiết)
Suy ra: ∆AIC = ∆BID (c.g.c)
Suy ra: ∠C = ∠D; ∠A1 = ∠B1 (1)
+) Lại có: ∠A1 + ∠A2 = 180º (hai góc kề bù)
Và ∠B1 + ∠B2 = 180º (hai góc kề bù)
Suy ra: ∠A2 = ∠B2
+) Xét tam giác OAD và ∆ OBC có:
∠A2 = ∠B2 (chứng minh trên)
AD = BC (vì AI + ID = BI + IC)
∠D = ∠C (chứng minh trên)
Suy ra: ∆OAD = ∆ OBC (g.c.g)
Suy ra: OA = OB (hai cạnh tương ứng).