Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 12 c m 3 Tính thể tích của tứ diện AB'CD'
A. 2 c m 3 c m 3
B. 3 c m 3
C. 4 c m 3
D. 5 c m 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C

Ta có V A B ' C D ' = V A B C D . A ' B ' C ' D ' − V A B B ' C − V B ' C ' C D ' − V A D C D ' − V A A ' B ' D '
= 12 − 1 6 .4. V A B C D . A ' B ' C ' D ' = 12 − 1 6 .4.12 = 4

Tham khảo:
\( \Rightarrow ({x^3} + 8{x^2} + 19x + 12):(x + 3) =\) diện tích đáy
Ta có :

Vậy diện tích đáy là : \({x^2} + 5x + 4\) \(c{m^2}\)

Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .

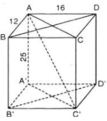
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 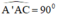
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Chọn C
Gọi S là diện tích đáy của tứ giác ABCD và h là chiều cao của khối hộp.
Chia khối hộp ABCD.A'B'C'D' thành khối tứ diện AB'CD' và 4 khối chóp AA'B'D', CB'C'D', B'.BAC, D'.DAC
Suy ra
Vậy V A B ' C D '