Cho hàm số y = 3 x + 1 x - 1 có đồ thị (C). Có bao nhiêu đường thẳng cắt (C) tại hai điểm phân biệt đều có tọa độ nguyên?
A. 30
B. 12
C. 15
D. 24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 11 2019
Chọn đáp án C.
Trước hết ta tìm số điểm có toạ độ nguyên thuộc (C), ta có
Do đó x , y ∈ ℤ
⇒ x - 1 ∈ ± 1 ; ± 2 ; ± 4 có tất cả có 6 điểm có toạ độ nguyên thuộc (C).
Đường thẳng cần tìm là đường thẳng đi qua 2 trong 6 điểm đã cho
vậy có tất cả C 6 2 = 15 đường thẳng thỏa mãn.
CM
23 tháng 6 2017
Gọi 
phương trình tiếp tuyến của (C) tại M là
Phương trình hoành độ giao điểm:
Yêu cầu bài toán tương đương với (1) có hai nghiệm phân biệt khác
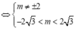
Vậy có tất cả 5 điểm có toạ độ nguyên thoả mãn.
Chọn đáp án A.
CM
18 tháng 7 2019
+ Phương trình hoành độ giao điểm của (C) và đường thẳng d:
=x4- (2m-1) x2+2m = 2 hay x4- (2m-1) x2+2m -2=0
Suy ra x2= 1 hoặc x2= 2m-2 (1)
+ Đường thẳng d cắt C tại bốn điểm phân biệt có hoành độ nhỏ hơn 3 khi và chỉ khi phương trình (1) có hai nghiệm phân biệt nhỏ hơn 3.
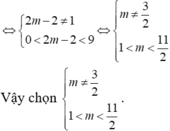
Do đó có 4 giá trị nguyên của m thỏa mãn đầu bài.
Chọn D.
CM
19 tháng 3 2019
Đáp án D
Phương trình hoành độ giao điểm của C và d là
x x − 1 = m − x ⇔ x ≠ 1 x 2 − m x + m = 0 * .
Để C cắt d tại hai điểm phân biệt ⇔ * có hai nghiệm phân biệt khác 1 ⇔ m > 4 m < 0 .
Khi đó, gọi điểm A x 1 ; m − x 1 và B x 2 ; m − x 2 là giao điểm của đồ thị C và d .
⇒ O A = 2 x 1 2 − 2 m . x 1 + m 2 = 2 x 1 2 − m x 1 + m + m 2 − 2 m = m 2 − 2 m O B = 2 x 2 2 − 2 m . x 2 + m 2 = 2 x 2 2 − m x 2 + m + m 2 − 2 m = m 2 − 2 m
Khoảng cách từ O đến AB bằng
h = d O ; d = m 2 ⇒ S Δ A B C = 1 2 . h . A B = m 2 2 . A B
Ta có
S Δ A B C = a b c 4 R ⇔ R = a b c 4. S Δ A B C = O A . O B . A B 2. h . A B = O A . O B 2. h ⇔ 4 2 . m 2 = O A . O B ⇔ O A 2 . O B 2 = 16 m 2
Khi đó m 2 − 2 m 2 = 16 m 2 ⇔ m 2 − 2 m = 4 m m 2 − 2 m = − 4 m ⇔ m = 0 m = − 2 m = 6 .
Kết hợp với điều kiện m > 4 m < 0 , ta được m = − 2 m = 6 là giá trị cần tìm
TH
21 tháng 4 2016
Phương trình hoành độ giao điểm \(3x^2+2mx+3m-4=0\left(1\right)\) với x. Đường thẳng d cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\begin{cases}9m^2-36m+48>0\\0.m-1\ne0\end{cases}\) (đúng với mọi m)
Gọi \(x_1;x_2\) là các nghiệm của phương trình (1), ta có : \(\begin{cases}x_1+x_2=-m\\x_1x_2=\frac{3m-4}{3}\end{cases}\) (*)
Giả sử \(A\left(x_1;x_1+m\right);B\left(x_2;x_2+m\right)\)
Khi đó ta có \(OA=\sqrt{x^2_1+\left(x_1+m\right)^2};OA=\sqrt{x^2_2+\left(x_2+m\right)^2}\)
Kết hợp (*) ta được \(OA=OB=\sqrt{x_1^2+x_2^2}\)
Suy ra tam giác OAB cân tại O
Ta có \(AB=\sqrt{2\left(x_1-x_2\right)^2}\). Tam giác OAB đều \(\Leftrightarrow OA^2=AB^2\Leftrightarrow x_1^2+x_2^2=2\left(x_1-x_2\right)^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Leftrightarrow m^2-6m+8=0\Leftrightarrow m=2\) hoặc m=4
CM
24 tháng 5 2017
Đáp án D
Phương trình hoành độ giao điểm của )C) và(d) là
x + 2 x = x + m ⇔ x ≠ 0 x 2 + m − 1 x − 2 = 0 *
Để (C) cắt (d) tại 2 điểm phân biệt ⇔ * có 2 nghiệm phân biệt khác 0 ⇔ m ∈ ℝ
Khi đó, gọi A x 1 ; x 1 + 1 ; B x 2 ; x 2 + m ⇒ x 1 + x 2 = 1 − m là tọa độ giao điểm của (C) và(d)
Ta có: A B → = x 2 − x 1 ; x 2 − x 1 ⇒ u A B → = 1 ; 1 ; trung điểm AB là: I 1 − m 2 ; 1 + m 2
m = 0 ⇒ M , A , B thẳng hang (loại m = 0 )
Phương trình trung trực là: x + y − 1 = 0
Do M ∈ d ⇒ Δ M A D luôn cân tại M
Kết hợp với m ∈ ℤ và có 2018 giá trị m cần tìm
Trước hết ta tìm số điểm có toạ độ nguyên thuộc (C), ta có
y = 3 x + 1 x - 1 = 3 ( x - 1 ) + 4 x - 1 = 3 + 4 x - 1
Do đó x , y ∈ ℤ ⇔ x - 1 ∈ ± 1 ; ± 2 ; ± 4 ⇒ có tất cả có 6 điểm có toạ độ nguyên thuộc (C). Đường thẳng cần tìm là đường thẳng đi qua 2 trong 6 điểm đã cho, vậy có tất cả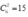
đường thẳng thỏa mãn.
Chọn đáp án C.