Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = trên đoạn [-1; 1].
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

Trên đoạn [-1; 1], ta có :
y = log 5 x
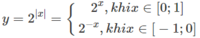
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - ( - 1 ) = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.

y = x 2 + 2 x + m - 4 = ( x + 1 ) 2 + m - 5
Ta có ( x + 1 ) 2 + m - 5 ∈ m - 5 ; m - 1
Giá trị lớn nhất của hàm số y = x 2 + 2 x + m - 4 trên đoạn[ -2; 1] đạt giá trị nhỏ nhất khi
m - 5 < 0 m - 1 > 0 5 - m = m - 1 ⇔ m = 3
Chọn B.

Ta có y = x 2 + 2 x + a - 4 = x + 1 2 + a - 5
Đặt u = x + 1 2 khi đó ∀ x ∈ - 2 ; 1 thì u ∈ 0 ; 4
Ta được hàm số f u = u + a - 5
Khi đó
M a x x ∈ - 2 ; 1 y = M a x x ∈ 0 ; 4 f u = M a x f 0 , f 4 = M a x a - 5 ; a - 1
Trường hợp 1:
a - 5 ≤ a - 1 ⇔ a ≤ 3 ⇒ M a x x ∈ 0 ; 4 f u = 5 - a ≥ 2 ⇔ a = 3
Trường hợp 2:
a - 5 ≤ a - 1 ⇔ a ≥ 3 ⇒ M a x x ∈ 0 ; 4 f u = a - 1 ≥ 2 ⇔ a = 3
Vậy giá trị nhỏ nhất của M a x x ∈ - 2 ; 1 y = 2 ⇔ a = 3
Đáp án A
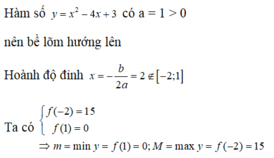

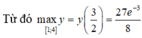
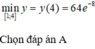
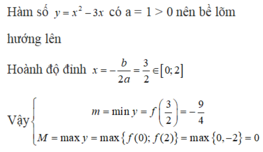
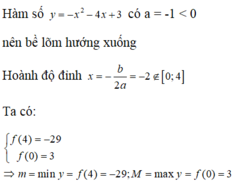
Trên đoạn [-1; 1], ta có :
y = log 5 x
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2 - - 1 = 2 1 = 2, y(0) = 2 0 = 1, y(1) = 2 1 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.