Cho hàm số
y
=
x
4
-
2
(
m
+
1
)
x
2
+
m
(
C
)
. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại A.
m
=
2
±
2
2
B.
...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m ( C ) . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại
A. m = 2 ± 2 2
B. m = 2 + 2 2
C. m = 2 - 2 2
D. m = ± 1
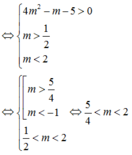
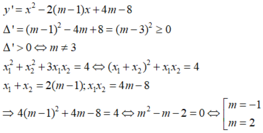
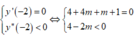
(không tồn tại m).
Chọn A
Ta có:
Hàm số có 3 điểm cực trị khi và chỉ khi :
y ' có 3 nghiệm phân biệt
⇔ m + 1 > 0 ⇔ m > - 1 ( * )
Khi đó, ta có y ' = 0
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử
Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1
Do đó OA = BC
⇔ m = 2 ± 2 2 ( t h ỏ a m ã n ) ( * )
Vậy m = 2 ± 2 2