GTNN của hàm số y = x 3 + 3 x 2 - 9 x + 1 trên đoạn [-4;4] là
A. -4
B. 1
C. 4
D. -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2021
\(a,\dfrac{x^2+x+2}{\sqrt{x^2+x+1}}=\dfrac{x^2+x+1+1}{\sqrt{x^2+x+1}}=\sqrt{x^2+x+1}+\dfrac{1}{\sqrt{x^2+x+1}}\left(1\right)\)
Áp dụng BĐT cosi: \(\left(1\right)\ge2\sqrt{\sqrt{x^2+x+1}\cdot\dfrac{1}{\sqrt{x^2+x+1}}}=2\)
Dấu \("="\Leftrightarrow x^2+x+1=1\Leftrightarrow x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
D
0
QM
1
CM
19 tháng 2 2019
* Hàm số đã cho liên tục trên R vì với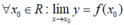 
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x 2 - 2 | x | + 2 = 0 vô nghiệm nên đồ thị không cắt trục hoành.
f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Chọn B
15 tháng 9 2023
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
CM
27 tháng 12 2019
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
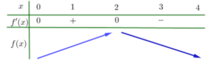
Từ bảng biến thiên, ta có nhận xét sau: 
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
17 tháng 9 2023
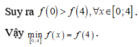
1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)
TK
0
CM
21 tháng 8 2018
Ta có
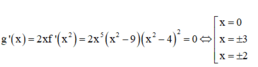
Bảng biến thiên của hàm số y= g( x)
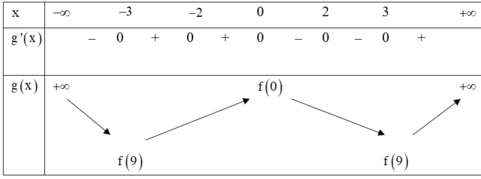
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.
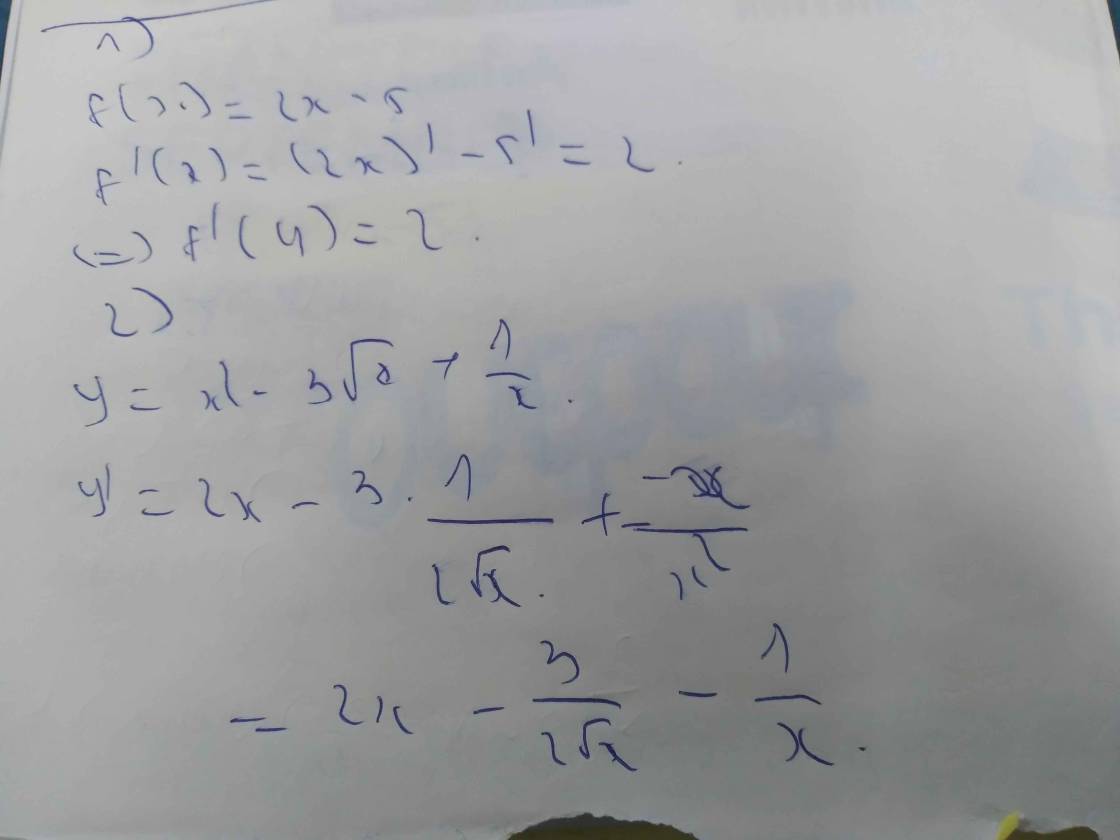
Chọn A
Xét hàm số y = x 3 + 3 x 2 - 9 x + 1 trên đoạn [-4;4].
Ta có:
y(1) = -4, y(-3) = 28; y(4) = 77; y(-4) = 21
GTNN của hàm số y = x 3 - 9 x + 1 trên đoạn [-4;4] là -4 khi x= 1