Cho hình chóp S.ABC có các cạnh SA = SB = SC = BA = BC = a . Tìm thể tích lớn nhất của hình chóp S.ABC
A. a 3 16
B. a 3 4
C. 2 a 3 3
D. a 3 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

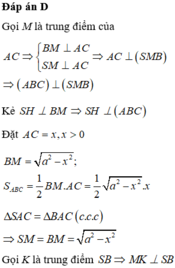
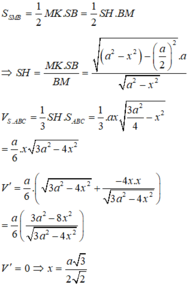
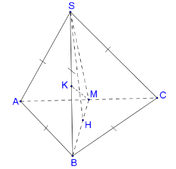

Đáp án D
Đặt A C = x x > 0
Gọi H là trung điểm của AC khi đó B H ⊥ A C S H ⊥ A C
Suy ra A C ⊥ S H B . Gọi E là trung điểm của SB ta có: C E = A E = a 3 2 .
Do tam giác EAC cân tại E nên
E H ⊥ A C ⇒ H E = C E 2 − C H 2 = 3 a 2 4 − x 2 4 .
Ta có: V A B C D = V C . S H B + V A . S H B = 1 3 . A C . S S H B = 1 3 x . 3 a 2 4 − x 2 4 . a 2
Lại có 3 a 2 4 − x 2 4 . x = 2. 3 a 2 4 − x 2 4 . x 2 ≤ 3 a 2 4 − x 2 4 + x 2 4
= 3 a 2 4 ⇒ V S . A B C ≤ a 3 8 ⇒ V m ax = a 3 8 .
Dấu bằng xảy ra ⇔ 3 a 2 = 2 x 2 ⇔ x = a 6 2 .

Đáp án C
S S A B = 1 2 S A . S B sin ≤ S A . S B ; d C l S A B ≤ S C
Khối chóp S.ABC có thể tích lớn nhất
S A ⊥ S B ⊥ S C ⇒ V max = 1 6 S A . S B . S C = a 3