Cho phương trình m. sin x + 4. cos x = 2m - 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
A. 4
B. 7.
C. 6.
D. 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
28 tháng 1 2019
Đúng(0)
Những câu hỏi liên quan
CM
14 tháng 3 2017
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
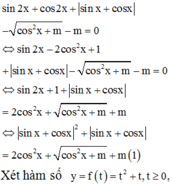
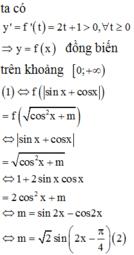
Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
16 tháng 5 2021
1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m
CM
18 tháng 5 2019
Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.
27 tháng 12 2021
https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha
