Giải bất phương trình ta được tập nghiệm là T. Tìm T
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1

=>2x^2-3x-4x+6+3x+8<2x^2+4x+2-4x
=>2x^2-4x+14<2x^2+2
=>-4x<-12
=>x>3
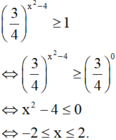
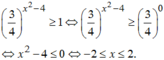


Đáp án A.
Ta có:
3 4 x 2 − 4 ≥ 1 ⇔ 3 4 x 2 − 4 ≥ 3 4 0 ⇔ x 2 − 4 ≤ 0 ⇔ − 2 ≤ x ≤ 2.