Cho tam giác MNP vuông tại M có MN = 12cn, NP = 20cm. Tính MP và gốc P (làm tròn đến độ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(NP=\sqrt{MN^2+MP^2}=10\left(cm\right)\)
b: Xét ΔMNP vuông tại M có MH là đường cao
nên MH*NP=MN*MP
=>MH*10=6*8=48
=>MH=4,8cm
Xét ΔMNP có MD là phân giác
nên \(MD=\dfrac{2\cdot6\cdot8}{6+8}\cdot cos45=\dfrac{24}{7}\sqrt{2}\left(cm\right)\)
c: MN*sinP+MP*sinN
=MN*MN/NP+MP*MP/NP
=(MN^2+MP^2)/NP
=NP^2/NP
=NP

MN+MP+NP=180
MN+MP+80=180cm
MP-MN=20cm
MN+MP=100cm
a.ĐỘ DÀI CẠNH MP LÀ: ((MN+MP)+(MP-MN))÷2=(100+20)÷2=60cm( tổng và hiệu)
Độ dài cạnh MN là: MP-20= 60-20=40cm
b. Diện tích tam giác vuông MNP là: 1/2× MN x MP=1/2 × 40 × 60= 1200cm2
Tổng độ dài của cạnh MN và MP là:
180 - 80 = 100(cm)
Độ dài cạnh MN là:
(100 - 20): 20 = 40(cm)
Độ dài cạnh MP là:
100 - 40 = 60(cm)
Diện tích tam giác MNP là:
40x60:2 = 1200(cm2)
Đ/S:..............

a: NP=10cm
C=MN+MP+NP=24(cm)
b: Xét ΔMNK vuông tại M và ΔENK vuông tại E có
NK chung
\(\widehat{MNK}=\widehat{ENK}\)
Do đó: ΔMNK=ΔENK
c: Ta có: MK=EK
mà EK<KP
nên MK<KP

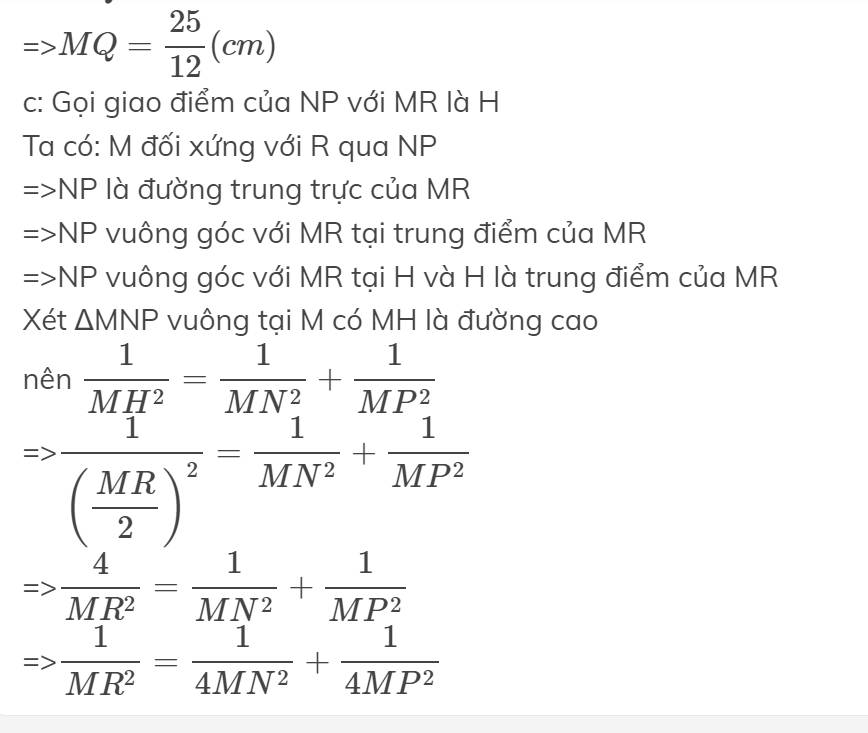
Áp dụng PTG: \(MP=\sqrt{NP^2-MN^2}=16\left(cm\right)\)
\(\sin P=\dfrac{MN}{NP}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{P}\approx37^0\)