Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


12 - √x - x
= 16 - x - 4 - √x (tách 12 = 16 - 4 và đổi vị trí)
= [42 - (√x)2] - (4 + √x)
= (4 - √x)(4 + √x) - (4 + √x)
= (4 + √x)(4 - √x - 1)
= (4 + √x)(3 - √x)

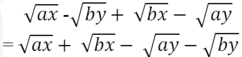
= √x(√a + √b) - √y(√a + √b)
= (√a + √b)(√x - √y) (với x, y, a và b đều không âm)

ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1)
= b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)

a) xy - y√x + √x - 1
= (√x)2.y - y√x + √x - 1
= y√x(√x - 1) + √x - 1
= (√x - 1)(y√x + 1) với x ≥ 1
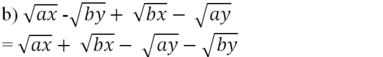
= √x(√a + √b) - √y(√a + √b)
= (√a + √b)(√x - √y) (với x, y, a và b đều không âm)
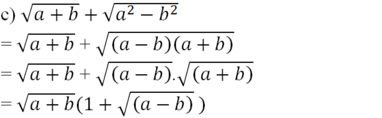
(với a + b, a - b đều không âm)
d) 12 - √x - x
= 16 - x - 4 - √x (tách 12 = 16 - 4 và đổi vị trí)
= [42 - (√x)2] - (4 + √x)
= (4 - √x)(4 + √x) - (4 + √x)
= (4 + √x)(4 - √x - 1)
= (4 + √x)(3 - √x)

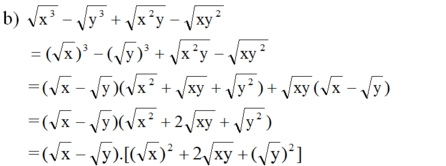
= (√x - √y)(√x + √y)2
= (√x - √y)(√x + √y)(√x + √y)
= (x - y)(√x + √y)

a, \(ab+b\sqrt{a}+\sqrt{a}+1=\sqrt{a}b\left(\sqrt{a}+1\right)+\sqrt{a}+1\)
\(=\left(b\sqrt{a}+1\right)\left(\sqrt{a}+1\right)\)
b, \(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}\)
\(=\sqrt{x^2}\left(\sqrt{x}+\sqrt{y}\right)-\sqrt{y^2}\left(\sqrt{y}+\sqrt{x}\right)=\left(\left|x\right|-\left|y\right|\right)\left(\sqrt{x}+\sqrt{y}\right)\)

a) ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1)
= b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)
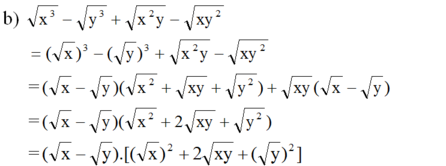
= (√x - √y)(√x + √y)2
= (√x - √y)(√x + √y)(√x + √y)
= (x - y)(√x + √y)

với a,b,x,y không âm ta có
a,\(ab+b\sqrt{a}+\sqrt{a}+1\)
\(=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)
b, \(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)+\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)^2\)
xy - y√x + √x - 1
= (√x)2.y - y√x + √x - 1
= y√x(√x - 1) + √x - 1
= (√x - 1)(y√x + 1) với x ≥ 1