Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giao điểm với trục tung B(0 ;-1). Ta có
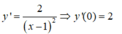
Hệ số góc của tiếp tuyến của đồ thị hàm số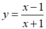 
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Chọn B
Chọn A.
Ta có y’ = x2 + 2x và y” = 2x + 2
Theo giả thiết xo là nghiệm của phương trình y”(xo) = 0
⇔ 2x + 2 = 0 ⇔ xo = -1
Và y’(-1) = -1
Phương trình tiếp tuyến tại điểm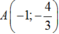 
là: y = -1.(x + 1) - 7/3
Hay 
.
Đáp án A
Hệ số góc của tiếp tuyến của đồ thị hàm số chính là đạo hàm cấp 1
Ta có y = − x 3 − 3 x 2 + 2 ⇒ y ' = − 3 x 2 − 6 x ⇒ y ' ' = − 6 x − 6
Phương trình y ' ' = 0 ⇔ x = − 1
Vậy hệ số góc cần tìm là k = y ' 1 = 3
Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y= x4-2x2+2
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y= kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
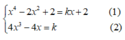
có nghiệm
Thay (2) vào (1) ta suy ra được
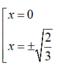
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
- Gọi d là tiếp tuyến của đồ thị hàm số đã cho qua A( 0, 2)
→ phương trình của d có dạng: y = k(x - 0) + 2 hay y = kx + 2
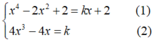
- Thay (2) vào (1) ta được :
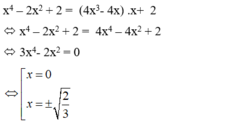
- Tương ứng với ba giá trị của x ta vừa tìm được, ta viết được 3 tiếp tuyến đi qua Ađến đồ thị (C).
Chọn B.
Ta có y ' = x 2 + 2 x và y" = 2x + 2.
- Theo giả thiết x 0 là nghiệm của phương trình y " ( x 0 ) = 0 .
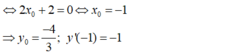
- Phương trình tiếp tuyến tại điểm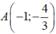 
là:
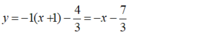
Chọn A.
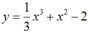
Chọn C