Cho tam giác ABC vuông tại A, có D là trung điểm của BC. Qua D vẽ DE ,DF lần lươt song song với AB,AC ( E thuộc AC, F thuộc AB)
a) Chứng minh tứ giác AEDF là hình chữ nhật.
b) Gọi M là điểm đối xứng với D qua AC. Chứng minh tứ giác AMCD là hình thoi.
c) Vẽ AH vuông góc với BC tại H. Chứng minh tứ giác HEFD là hình thang cân.
d) Gọi K là điểm đối xứng với A qua D. Tìm điều kiện của tam giác ABC để tứ giác ABKC là hình vuông.
Giúp mình bài này với!!!

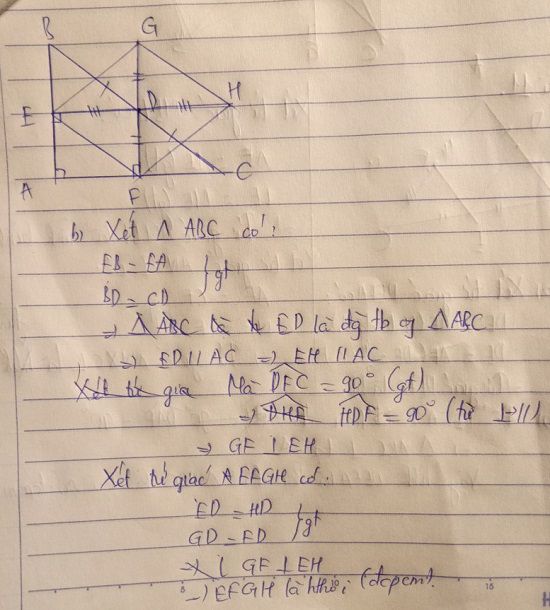

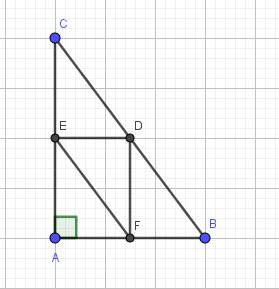
a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A