Cho dãy số u n v ớ i u n = 4 n - 2 ( n ≥ 1 ) . Xét tính tăng hay giảm của hàm số.
A. Dãy (un) tăng
B. Dãy (un) tăng
C. Dãy (un) không tăng, không giảm
D. Dãy (un) không đổi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2023
\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng
15 tháng 10 2023
a: \(\dfrac{u_n}{u_{n-1}}=\dfrac{3^n}{2^{n+1}}:\dfrac{3^{n-1}}{2^n}\)
\(=\dfrac{3^n}{3^{n-1}}\cdot\dfrac{2^n}{2^{n+1}}=\dfrac{3}{2}>1\)
=>(un) là dãy tăng
c: ĐKXĐ: n>=1
\(u_n=\sqrt{n}-\sqrt{n-1}\)
\(=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}\)
\(\dfrac{u_n}{u_{n-1}}=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}:\dfrac{1}{\sqrt{n-1}+\sqrt{n-2}}\)
\(=\dfrac{\sqrt{n-1}+\sqrt{n-2}}{\sqrt{n-1}+\sqrt{n}}< 1\)
=>Đây là dãy số giảm
CM
26 tháng 9 2019
Xét hiệu: u n + 1 − u n = 2 n + 1 n + 4 − 2 n − 1 n + 3
= 2 n 2 + 7 n + 3 − 2 n 2 − 7 n + 4 n + 4 n + 3 = 7 n + 4 n + 3 > 0 ; ∀ n ∈ N *
Vậy: ( u n ) là dãy số tăng.
Ta có u n = 2 n − 1 n + 3 = 2 ( n + 3 ) − 7 n + 3 = 2 − 7 n + 3
Suy ra: ∀ n ∈ ℕ * , u n < 2 nên ( u n ) bị chặn trên.
Vì ( u n ) là dãy số tăng ∀ n ∈ ℕ * , u 1 = 1 4 ≤ u n nên ( u n ) bị chặn dưới. Vậy ( u n ) bị chặn.
Chọn đáp án C.
NM
1
10 tháng 9 2023
\(u_n=\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}=\dfrac{3^{n+1}-1}{2^{n+1}}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{3^{n+1}-1}{2^{n+1}}-\dfrac{3^n-1}{2^n}\)
\(\Rightarrow u_{n+1}-u_n=\dfrac{2^n.3^{n+1}-2^n-2^{n+1}.3^n+2^{n+1}}{2^n.2^{n+1}}\)
\(=\dfrac{2^n.3^n\left(3-2\right)-2^n\left(2-1\right)}{2^{2n+1}}\)
\(=\dfrac{2^n.\left(3^n-1\right)}{2^{2n+1}}\)
\(=\dfrac{\left(3^n-1\right)}{2}>0\left(n>1\right)\)
Vậy dãy \(u_n\)đã cho tăng
PT
1
CM
9 tháng 2 2018
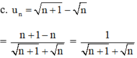
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
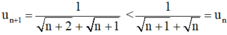
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
CM
20 tháng 5 2019
Ta có u n = n − 1 n + 1 = 1 − 2 n + 1
Xét hiệu u n + 1 − u n = 1 − 2 n + 2 − 1 − 2 n + 1
= 2 n + 1 − 2 n + 2 = 2 ( n + 2 ) − 2 ( n + 1 ) ( n + 1 ) . ( n + 2 ) = 2 ( n + 1 ) ( n + 2 ) > 0 ∀ n ∈ ℕ *
Kết luận dãy số ( u n ) là dãy số tăng.
Chọn đáp án D.
NM
1
10 tháng 9 2023
\(u_n=\sqrt[]{n+10}-\sqrt[]{n+2}\)
\(\Leftrightarrow u_n=\dfrac{n+10-\left(n+2\right)}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Leftrightarrow u_n=\dfrac{8}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(u_{n+1}=\sqrt[]{n+11}-\sqrt[]{n+3}\)
\(\Leftrightarrow u_{n+1}=\dfrac{n+11-\left(n+3\right)}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(\Leftrightarrow u_{n+1}=\dfrac{8}{\sqrt[]{n+11}+\sqrt[]{n+3}}\)
\(u_{n+1}-u_n=8\left(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}-\dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\right)\)
mà \(\dfrac{1}{\sqrt[]{n+11}+\sqrt[]{n+3}}< \dfrac{1}{\sqrt[]{n+10}+\sqrt[]{n+2}}\)
\(\Rightarrow u_{n+1}-u_n< 0\)
Vậy dãy đã cho là dãy số giảm
PT
1
Chọn A