Cho đường thẳng a và điểm A cách đường thẳng a một khoảng bằng 4cm. Trong các mặt cầu đi qua A và tiếp xúc với đường thẳng a, mặt cầu (S) có diện tích nhỏ nhất thì diện tích đó bằng:
A. 4π(c m 2 )
B. 16π/3(c m 2 )
C. 16π(c m 2 )
D. 64π(c m 2 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

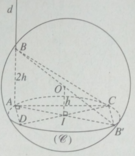
Diện tích tam giác BCD bằng:
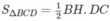
Diện tích này lớn nhất khi AI // CD.

Chọn A.
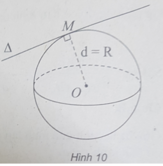
(h.10) Đường thẳng ∆ tiếp xúc với mặt cầu S(O;R) khi d = R.
Đáp án C
Gọi S(I ;r) là mặt cầu đi qua A và tiếp xúc với a.
Ta có diện tích của mặt cầu là : S = 4π r 3 nên S đạt giá trị nhỏ nhất khi và chỉ khi r đạt giá trị nhỏ nhất.
Gọi tiếp điểm của đường thẳng a và mặt cầu là H và hình chiếu vuông góc hạ từ A lên đường thẳng A là A’. Khi đó ta có:
2r = IA + IH ≥ AH ≥ AA' => r ≥ AA'/2 = 2(cm)
Vậy r đạt giá trị nhỏ nhất bằng 2cm khi I là trung điểm của AA’.
Khi đó mặt cầu (S) có diện tích nhỏ nhất là S = 4π 2 2 = 16π(c m 2 ).