Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa hai đường thẳng AC và A’D.
A. 45 ∘
B. 30 ∘
C. 60 ∘
D. 90 ∘
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
G
10 tháng 8 2023
\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A
CM
14 tháng 9 2018
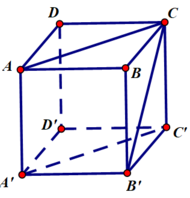
a) Góc giữa AB và B’C’ = góc giữa AB và BC (vì B’C’//BC)
⇒ Góc giữa AB và B’C’ = A B C ^ = 90 o
b) Góc giữa AC và B’C’ = góc giữa AC và BC (vì B’C’//BC)
⇒ Góc giữa AC và B’C’ = A C B ^ = 45 o
c) Góc giữa A’C’ và B’C = góc giữa AC và B’C (vì A’C’//AC)
ΔACB’ đều vì AC = B’C = AB’ (đường chéo của các hình vuông bằng nhau)
⇒ Góc giữa A’C’ và B’C = A C B ' ^ = 60 o
CM
22 tháng 8 2017
Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD – bằng góc ACD
Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D
⇒ A C D ^ = 45 0
Đáp án B
CM
24 tháng 2 2018
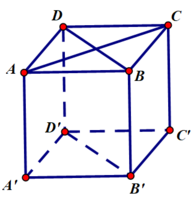
a) AD, A’D’, BC, B’C’, AA’, BB’, CC’, DD’
b) BD, B’D’, AA’, BB’, CC’, DD’
CM
25 tháng 1 2017
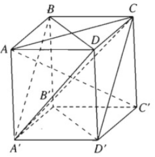
a) Ta có AB = AD = AA′ = a
và C ′ B = C ′ D = C ′ A ′ = a 2
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh A C = a 2 và CC’ = a
Vậy A C ′ 2 = A C 2 + C C ′ 2
⇒ A C ′ 2 = 2 a 2 + a 2 = 3 a 2 . V ậ y A C ′ = a 3 .