Cho lăng trụ ABC.A’B’C’. Gọi E, F, G lần lượt là trung điểm của AA’, BB’, CC’. Chứng minh rằng các lăng trụ ABC.EFG và EFG.A’B’C’ bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).

Chọn B
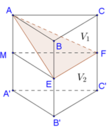
Gọi M là trung điểm của AA’. Gọi V là thể tích của hình lăng trụ ABC.A’B’C’
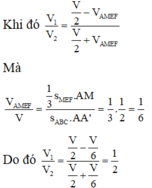

Chọn B
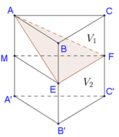
Gọi M là trung điểm của AA’. Gọi V là thể tích của hình lăng trụ ABC.A’B’C’
Khi đó
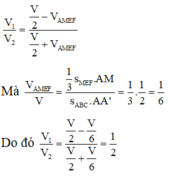

Chọn A.
Để ý rằng hai khối lăng trụ đó có diện tích đáy bằng nhau, tỉ số hai đường cao tương ứng bằng 1/2.
a.1/2
okkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

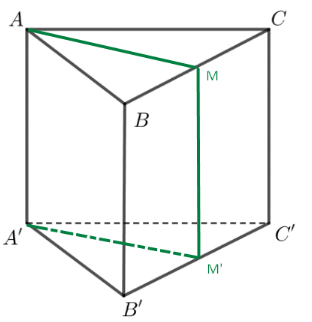
Ta có M, M' lần lượt là trung điểm của BC, B'C', BCC'B' là hình bình hành suy ra MM' // CC'.
Vì các cạnh bên của hình lăng trụ ABC.A'B'C' đôi một song song nên AA'//CC'.
Mặt phẳng ((AMC) //(A'M'C') nên AMC. AM'C' là hình lăng trụ.
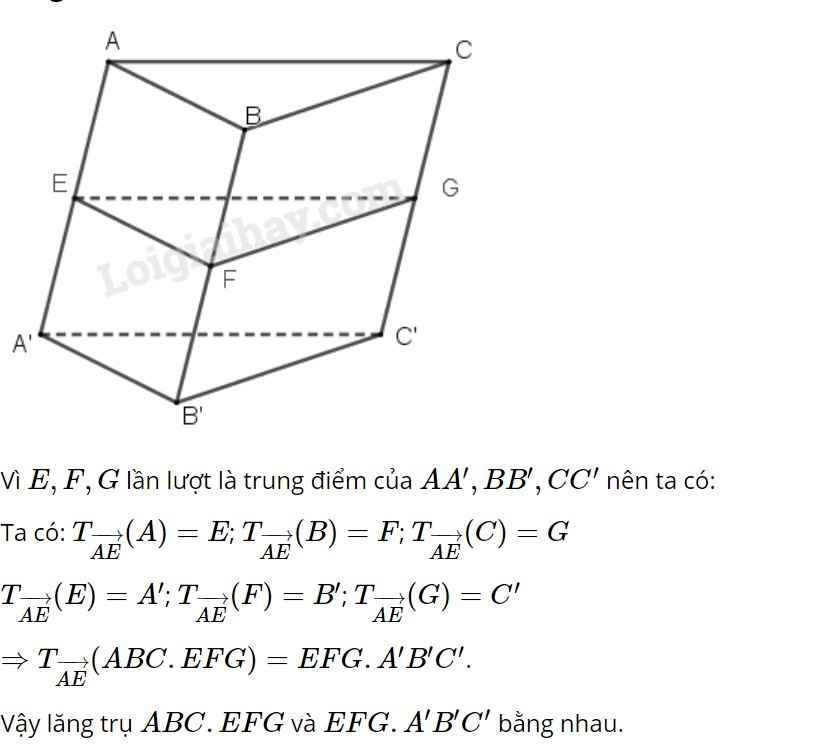


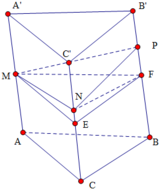
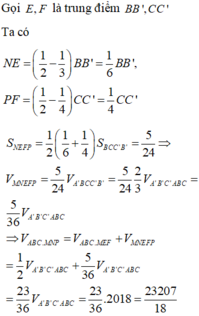
Dùng phép tịnh tiến vectơ AE → biến lăng trụ ABC.EFG thành lăng trụ EFG.A’B’C .