Cho đường tròn có bán kính bằng 4 và các nữa đường tròn có bán kính bằng 2 như hình vẽ. Khi quay hình tròn quanh cạnh AB thì các nửa đường tròn nhỏ sinh ra các khối tròn xoay có thể tích bằng bao nhiêu?
A. 71,6 π
B. 242,3 π
C. 62,5 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Đặt SA = h tam giác SAB vuông tại A ⇒ A B = S A tan 60 ° = h 3 .
Tam giác IAB vuông tại A ⇒ tan I B A ^ = I A A B ⇒ I A = h 3 .
Khi quay tam giác SAB quay trục SA, ta được khối nón có chiều cao h, bán kính r = h 3 ,
Và quay nửa đường tròn quanh trục SA, ta được khối cầu có bán kính R = h 3 .
Vậy V 1 = 1 3 πr 2 h = 1 3 π . h 3 2 h = πh 3 9 V 2 = 4 3 πR 2 = 4 3 π h 3 3 = 4 πh 3 81 ⇒ V 1 V 2 = 1 9 : 4 81 = 9 4 ⇒ 4 V 1 = 9 V 2 .

Đáp án B
Ta có diện tích tam giác cong ABC bằng 4 lần diện tích tam giác cong ADO
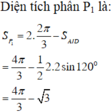
Vậy diện tích hình tam giác cong là:
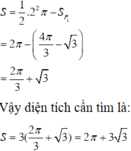

Đáp án B
Bán kính đường tròn ngoại tiếp tam giác là R = B C 2 sin A = 3 2 sin 60 = 3
Độ dài đường cao là A H = A B sin B 3 3 2
Khi quay quanh đường thẳng AD
Thể tích hình cầu tạo thành là V 1 = 4 3 π R 3 = 4 π 3
Thể tích khối nón tạo thành là V 1 = 1 3 π r 2 h = 1 3 π H B 2 . A H = 23 8 π 3

Đáp án B
Bán kính đường tròn ngoại tiếp tam giác là: R = B C 2 sin A = 30 2 sin 60 = 3
Độ dài đường cao là A H = A B sin B = 3 3 2
Khi quay quanh đường thẳng AD
Thể tích hình cầu tạo thành là: V 1 = 4 3 π R 3 = 4 π 3
Thể tích khối nón tạo thành là: V 2 = 1 3 π r 2 h = 1 3 π H B 2 . A H = 23 8 π 3

Chọn A.
Cho hình tròn đường kính 4a quay quanh đường kính của nó ta được khối cầu có đường kính 4a hay bán kính R = 2a.
Đáp án C