Mn giúp mình với ah
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


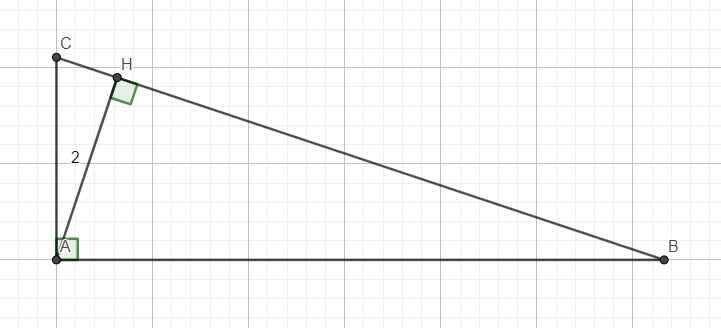
Xét \(\Delta HAB\) vuông tại H \(\left(AH\perp BC\right)\),ta có:
\(AB^2=AH^2+BH^2\left(ĐLPytago\right)\\ \Rightarrow BH^2=AB^2-AH^2\\ \Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{7^2-2^2}=3\sqrt{5}\left(cm\right)\)
Xét \(\Delta ABC\) vuông tại A và có AH là đường cao \(\left(AH\perp BC\right)\),ta có:
\(AH^2=BH.CH\left(HTL\right)\\ \Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{2^2}{3\sqrt{5}}=\dfrac{4\sqrt{5}}{15}\left(cm\right)\)

ΔABC vuông cân tại A⇒AB=AC=4
Áp dụng hệ thức lượng ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{4^2}+\dfrac{1}{4^2}\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{16}+\dfrac{1}{16}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{8}\\ \Rightarrow AH^2=8\\ \Rightarrow AH=\sqrt{8}\)
Vì ΔABC vuông cân tại A
⇒ AB = AC = 4 cm
Áp dụng dịnh lí Py-ta-go vào ΔABC vuông tại A ta có:
BC2=AB2+AC2=42+42=32
⇔BC=\(4\sqrt{2}\)
Ta có:AB.AC=AH.BC (hệ thức lượng)
⇔\(AH=\dfrac{AB.AC}{BC}=\dfrac{4.4}{4\sqrt{2}}=2\sqrt{2}\left(cm\right)\)

Ta có: \(\dfrac{HC}{AC}=\dfrac{1}{3}\)
nên AC=3HC
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AH^2+HC^2=AC^2\)
\(\Leftrightarrow9HC^2-HC^2=4^2=16\)
\(\Leftrightarrow HC=\sqrt{2}\left(cm\right)\)
\(\Leftrightarrow AC=3\cdot HC=3\sqrt{2}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H,ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=4^2+2^2=20\)
hay \(AB=2\sqrt{5}\left(cm\right)\)
Cho tam giác ABC vuông tại A, AH vuông góc với BC,có AH=2, tan B=1/3. Tính AB, AC. Mong mn giúp mình

Trong tam giác vuông ABH ta có:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=6\)
Áp dụng định lý Pitago:
\(AB^2=AH^2+BH^2=40\)
\(\Rightarrow AB=2\sqrt{10}\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AC=AB.tanB=\dfrac{2\sqrt{10}}{3}\)

x2 - 4x + 2 = ( x2 - 4x + 4 ) - 2 = ( x - 2 )2 - 2 ≥ -2 ∀ x
Dấu "=" xảy ra <=> x = 2 . Vậy GTNN của bthuc = -2
x^2 - 4x + 2
= x^2 - 4x + 4 - 2
= ( x - 2 ) ^2 - 2
\(\left(x-2\right)^2\ge0\forall x\)
\(\left(x-2\right)^2-2\ge-2\)
Dấu = xảy ra khi và chỉ khi
x - 2 = 0
x = 0 + 2
x = 2
vậy min = -2 khi và chỉ khi x = 2




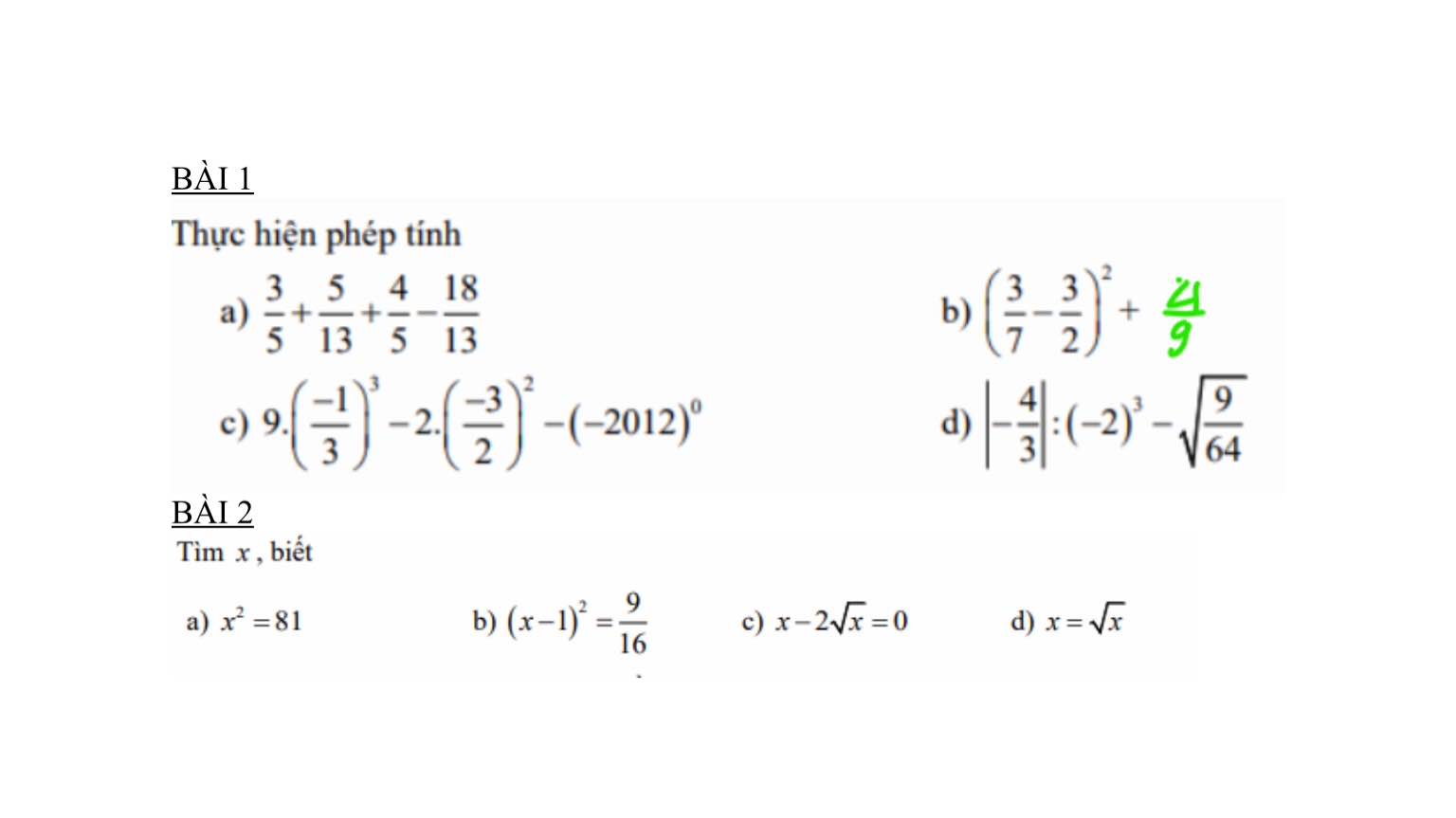 Mn lm giúp mình vs ah mình cần gấp !!!
Mn lm giúp mình vs ah mình cần gấp !!!