Trong không gian Oxyz, cho mặt cầu (S) có phương trình
x
2
+
y
2
+
z
2
= 1. Viết phương trình mặt phẳng (P) đi qua 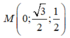 và tiếp xúc với (S)
và tiếp xúc với (S)
A. 3 x + 4z - 2 = 0
B. 3 y + z - 2 = 0
C. y + 3 z = 0
D. x + 3 y + z - 2 = 0

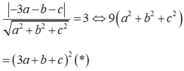
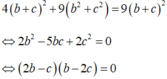





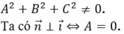
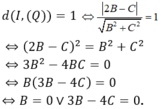
Đáp án B