Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
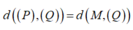
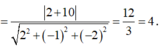
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
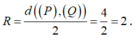
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
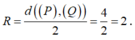
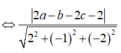
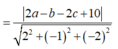
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
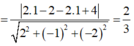
do đó tam giác AHI vuông tại H nên
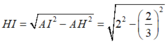
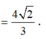
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
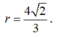
Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
Chọn D.
Mặt cầu (S) có tâm I(-1;2;1) và bán kính
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0 với D ≠ 1.
Vì (P) tiếp xúc với mặt cầu (S) nên d(I;(P)) = R = 3
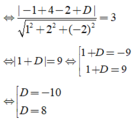
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0
Đáp án A
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n → (2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu: 2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4π R 2 = 4 π