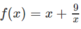giá trị nhỏ nhất của p đề p;p+3;p+8 đều là các số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 1 2019
Ta có A= \(\frac{3x-17}{4-x}=\frac{3x-12-5}{4-x}\)\(=\frac{3x-12}{4-x}-\frac{5}{4-x}=-3-\frac{5}{4-x}\)
=>A \(< -3\)
=> Để A đạt Min => \(\frac{5}{4-x}\) phải đạt Max => \(4-x\)phải đạt Min
có B=4-x \(\le\)4
(lại có đk : 4-x \(\ne\)0=> x\(\ne4;\)/ 4-x\(>\)0 ( do nếu 4-x <0 => A>-3 => chắc chắn không đạt Min)và \(x\ge0\)(do nếu x<0 => B>4 ( B không đạt Min)
=> \(0< 4-x\le4\) mà x là giá trị nguyên => B có giá trị nhỏ nhất = 1
=> x=3
khi x= 3 => A=-8
Sai thì bảo lại mình nhé
NV
0
HN
0
CM
22 tháng 1 2019
Chọn D
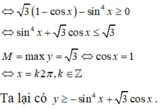
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có
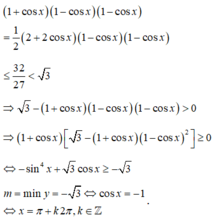
Do đó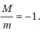 
. Vì vậy, mệnh đề D sai.
CM
7 tháng 11 2017
Ta có
sin 5 x ≤ sin 4 x ⇒ y ≤ sin 4 x + 3 cos x
Áp dụng bất đẳng thức Cauchy ta có:
1 - cos x 1 + cos x 1 + cos x = 1 2 2 - 2 cos x 1 + cos x 1 + cos x
≤ 1 2 2 - 2 cos x + ( 1 + cos x ) 2 3 3 = 32 27 < 3
⇒ 3 - 1 - cos x 1 + cos x 2 > 0 ⇒ 1 - cos x 3 - 1 - cos x 1 + cos x 2 ≥ 0 ⇒ 3 1 - cos x - sin 4 x ≥ 0 ⇔ sin 4 x + 3 cos x ≤ 3
M = maxy = 3 ⇔ cos(x) = 1
⇔ x = k 2 π , k ∈ ℤ
Ta lại có
y ≥ - sin 4 x + 3 cos x
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có:
1 + cos x 1 - cos x 1 - cos x = 1 2 2 + 2 cos x 1 - cos x 2 ≥ 32 27 ≤ 3 ⇒ 3 - 1 + cos x 1 - cos x 2 > 0 ⇒ 1 + cos x 3 - 1 + cos x 1 - cos x 2 ⇔ sin 4 x + 3 cos x ≥ - 3 m = m i n y = - 3 ⇔ cos x = - 1 ⇔ x = k 2 π , k ∈ ℤ
Do đó M m = - 1 . Vì vậy, mệnh đề D sai.
Đáp án cần chọn là D
CM
14 tháng 11 2017
Ta có
y = sin x = cos 2 x = sin x - 1 - 2 sin 2 x = 2 sin 2 x + sin x - 1
Đặt t = sin(x), - 1 ≤ t ≤ 1
Ta sẽ đi tìm GTLN và GTNN của hàm số y = g t = 2 t 2 + t - 1 trên đoạn [ -1;1 ]
Ta có g t = - 2 t 3 - t + 1 , - 1 ≤ t ≤ 1 2 2 t 3 + t - 1 , 1 2 ≤ t ≤ 1
* Xét hàm số h t = - 2 t 3 - t + 1 trên đoạn - 1 ; 1 2
Dễ dàng tìm được
M a x r ∈ 1 2 ; 1 h t = 9 8 ⇔ t = - 1 4 M i n r ∈ 1 2 ; 1 h t = 0 ⇔ t = 1 2
* Xét hàm số k t = 2 t 3 + t - 1 trên đoạn 1 2 ; 1
Cũng dễ dàng tìm được
M a x r ∈ 1 2 ; 1 k t = 2 ⇔ t = 1 M i n r ∈ 1 2 ; 1 k t = 0 ⇔ t = 1 2
Qua hai trường hợp trên ta đi đến kết luận
M a x r ∈ - 1 ; 3 g t = 2 ⇔ t = 1 M i n r ∈ - 1 ; 3 g t = 0 ⇔ t = 1 2
Hay
M = M a x y = 2 ⇔ sin x = - 1 ⇔ x = - π 2 + k 2 π m = Miny = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án C
CM
15 tháng 5 2017
TXĐ: D = R\{0}
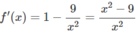
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:
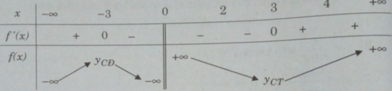
Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
TN
17 tháng 5 2023
TXĐ: D = R\{0}
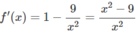
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:
Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
CM
15 tháng 7 2018
TXĐ: D = R\{0}
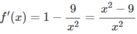
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:
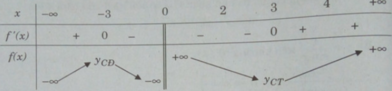
Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
