Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Ta có
Giải (1) , đặt f(x) = 2x - x - 1. Xét hàm số f(x) = 2x - x - 1trên R, có f’(x) = 2x.ln2 - 1
Phương trình
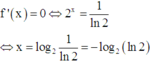
=> f(x) = 0 có nhiều nhất 2 nghiệm mà f(0) = f(1) => f(x) = 0 <=> x = 0 hoặc x = 1
Để phương trình đã cho có hai nghiệm phân biệt <=> (2) có 1 nghiệm hoặc 0
Vậy m = {0 ;1} là hai giá trị cần tìm.
Đáp án B.
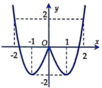
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x - m 2 x = x 2 - ( m - 1 ) x - m
⇔ x - m 2 x = ( x - m ) ( x + 1 ) ⇔ x - m 2 x - x - 1 = 0 ⇔ x = m 2 x = x + 1
Giải phương trình 2 x = x + 1 .
Nhìn vào màn hình ta thấy phương trình 2 x = x + 1 có hai nghiệm phân biệt là x = 0 ; x = 1 . Do vậy để tập nghiệm của phương trình đã cho có đúng hai phần tử thì m ∈ 0 ; 1 . Vậy có 2 giá trị của m thỏa mãn, ta chọn B.
Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
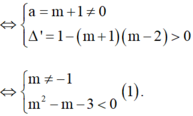
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
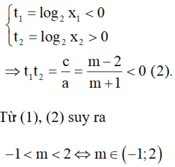
Đáp án D
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x . 2 x = x 2 - m x + x + m . 2 x - m
⇔ 2 x x - m = x + 1 x - m ⇔ 2 x - x - 1 x - m = 0 ⇔ [ 2 x - x - 1 = 0 ( 1 ) x - m = 0 ( 2 )
Giải (1) , đặt f x = 2 x - x - 1 . Xét hàm số f x = 2 x - x - 1 trên ℝ , có f ' x = 2 x . ln 2 - 1
Phương trình f ' x = 0 ⇔ 2 x = 1 ln 2 ⇔ x = log 2 1 ln 2 = - log 2 ln 2
⇒ f x = 0 có nhiều nhất 2 nghiệm mà f 0 = f 1 ⇒ f x = 0 ⇔ [ x = 0 x = 1
Để phương trình đã cho có hai nghiệm phân biệt ⇔ 2 có 1 nghiệm hoặc 0
Vậy m = {0;1} là hai giá trị cần tìm.