Giá trị lớn nhất của hàm số y = s i n 2 x + 2 c o s x + 2 là
A. 2
B. 0
C. 4
D. 5 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 5 2019
Đúng(0)
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
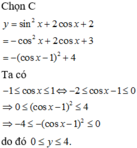
Lời giải:
a. $y=\sqrt{x^2+x-2}\geq 0$ (tính chất cbh số học)
Vậy $y_{\min}=0$. Giá trị này đạt tại $x^2+x-2=0\Leftrightarrow x=1$ hoặc $x=-2$
b.
$y^2=6+2\sqrt{(2+x)(4-x)}\geq 6$ do $2\sqrt{(2+x)(4-x)}\geq 0$ theo tính chất căn bậc hai số học
$\Rightarrow y\geq \sqrt{6}$ (do $y$ không âm)
Vậy $y_{\min}=\sqrt{6}$ khi $x=-2$ hoặc $x=4$
$y^2=(\sqrt{2+x}+\sqrt{4-x})^2\leq (2+x+4-x)(1+1)=12$ theo BĐT Bunhiacopxky
$\Rightarrow y\leq \sqrt{12}=2\sqrt{3}$
Vậy $y_{\max}=2\sqrt{3}$ khi $2+x=4-x\Leftrightarrow x=1$
c. ĐKXĐ: $-2\leq x\leq 2$
$y^2=(x+\sqrt{4-x^2})^2\leq (x^2+4-x^2)(1+1)$ theo BĐT Bunhiacopxky
$\Leftrightarrow y^2\leq 8$
$\Leftrightarrow y\leq 2\sqrt{2}$
Vậy $y_{\max}=2\sqrt{2}$ khi $x=\sqrt{2}$
Mặt khác:
$x\geq -2$
$\sqrt{4-x^2}\geq 0$
$\Rightarrow y\geq -2$
Vậy $y_{\min}=-2$ khi $x=-2$
26 tháng 10 2018
a)
x2 - 2x + 3 = (x2 - 2x + 1) + 2
= (x - 1)2 + 2 >= 2
Vậy min = 2 => Chọn B
b)
4x - 4x2 = -(1 - 2.2x + (2x)2) + 1
= -(1 - 2x)2 + 1 bé hơn hoặc bằng 1
Vay max = 1 => Chọn C
28 tháng 10 2023
\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)
\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)
\(f'\left(x\right)=0\)
=>\(cosx\left(sinx+2\right)=0\)
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)
nên \(x=\dfrac{\Omega}{2}\)
\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)
=1+4-5=0
\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)
=>Chọn D
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 1 2022
\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)