Tìm m để hàm số y = f x = x 2 3 x - 2 x

PT

Pham Trong Bach

8 tháng 1 2019

Tìm m để hàm số y = f x = x 2 + 3 x - 2 x - 1 k h i x > 1 m x + 2 k h i x ≤ 1 liên tục tại x = 1 A. m = - 3 2 B. m = 3 4 C. m = -3 D. m = - 3 4 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

8 tháng 1 2019

Đáp án D

Đúng(0)

KN

kim ngân

31 tháng 7 2021

Cho hàm số y=f(x)=\(\dfrac{1}{3}x^3\) - \(2x^2\) +mx +5. tìm m để;

f'(x)\(\ge\)0 \(\forall\)x\(\in i\)

#Toán lớp 11

1

TA

Trần Ái Linh

31 tháng 7 2021

`f'(x) = x^2 - 4x+m`

`f'(x) >=0 <=>x^2-4x+m>=0`

`<=> \Delta' >=0`

`<=> 2^2-1.m>=0`

`<=> m<=4`

Vậy....

Đúng(0)

CT

Chàng trai Nhân Mã

23 tháng 12 2023

a) (1- x2). ( 4x+5/x-1 - 9/x-1)b. x2 + xy - 2x - 2y Câu 5. Cho hàm số: y = (2m+1)x - 3 a. Với m=3. Tính f (-3); f(0) b. Tìm m để điểm A(2; 3) thuộc đồ thị hàm số. c. Vẽ đồ thị hàm số với m= 1 d. Tìm điều kiện để hàm số là hàm bậc nhất. e. Tìm m để hàm số song song với đường thẳng y= 5x+1...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 12 2023

Câu 5:

a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)

\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)

\(f\left(0\right)=7\cdot0-3=-3\)

b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:

\(2\left(2m+1\right)-3=3\)

=>2(2m+1)=6

=>2m+1=3

=>2m=2

=>m=1

c: Thay m=1 vào hàm số, ta được:

\(y=\left(2\cdot1+1\right)x-3=3x-3\)

*Vẽ đồ thị

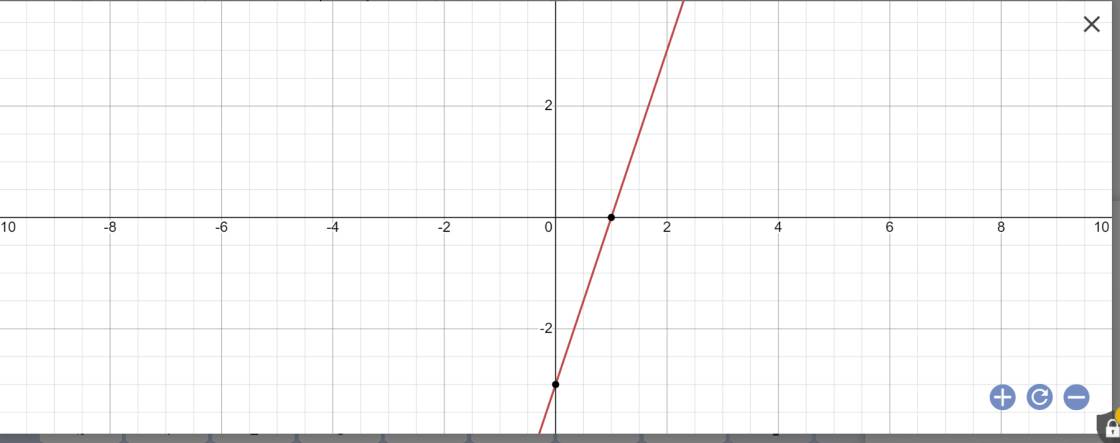
loading...

d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)

=>\(2m\ne-1\)

=>\(m\ne-\dfrac{1}{2}\)

e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)

=>2m+1=5

=>2m=4

=>m=2

Đúng(0)

TQ

Tố Quyên

13 tháng 11 2023

Cho hàm số y= F(x) = x×(x-2) và hàm số y= G(x) = -x+6

a) tính F(3); [ F(2/3) ]² ; G(-1/2)

b) tìm x để F(x)=0

c) tìm a để F(a)=G(a)

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

13 tháng 11 2023

a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)

\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)

\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)

\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)

b: F(x)=0

=>x(x-2)=0

=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

c: F(a)=G(a)

=>\(a\left(a-2\right)=-a+6\)

=>\(a^2-2a+a-6=0\)

=>\(a^2-a-6=0\)

=>(a-3)(a+2)=0

=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)

Đúng(2)

NT

nguyễn trần an bình

7 tháng 10 2021

cho hàm số y= f(x)=(m-3)x + m-2 a)tìm m để hàm số trên là hàm số đồng biến b) tìm m biết f(-1)=1

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 10 2021

a: Để hàm số đồng biến thì m-3>0

hay m>3

b: Thay x=-1 và y=1 vào (d), ta được:

-m+3+m-2=1

hay 1=1(đúng)

Đúng(0)

NT

nguyen thi be

8 tháng 4 2021

đạo hàm các hàm số sau:1.y=\(\dfrac{\sqrt{x+1}}{x}\)2.\(\dfrac{x}{1-x^2}\)3. y=\(\dfrac{1}{x-\sqrt{x+1}}\)cho f(x)=\(x^2+\dfrac{1}{x^2}\) tìm x để y'=0y=\(\sqrt{1+\sqrt{1+x}}\) tìm x để...

Đọc tiếp

#Toán lớp 11

1

HT

Hoàng Tử Hà

8 tháng 4 2021

1/ \(y'=\dfrac{\left(\sqrt{x+1}\right)'x-x'\sqrt{x+1}}{x^2}=\dfrac{\dfrac{x}{2\sqrt{x+1}}-\sqrt{x+1}}{x^2}=\dfrac{-x-2}{2x^2\sqrt{x+1}}\)

2/ \(y'=\dfrac{1-x^2-\left(1-x^2\right)'x}{\left(1-x^2\right)^2}=\dfrac{1+x^2}{\left(1-x^2\right)^2}\)

3/ \(y'=\dfrac{-\left(x-\sqrt{x+1}\right)'}{\left(x-\sqrt{x+1}\right)^2}=\dfrac{-1+\dfrac{1}{2\sqrt{x+1}}}{\left(x-\sqrt{x+1}\right)^2}\)

4/ \(y'=f'\left(x\right)=2x-\dfrac{2x}{x^4}=2x-\dfrac{2}{x^3}\)

\(y'=0\Leftrightarrow\dfrac{2x^4-2}{x^3}=0\Leftrightarrow x=\pm1\)

5/ \(y'=\dfrac{\dfrac{1}{2\sqrt{1+x}}}{2\sqrt{1+\sqrt{1+x}}}\Rightarrow f\left(x\right).f'\left(x\right)=\sqrt{1+\sqrt{1+x}}.\dfrac{1}{4\sqrt{1+x}.\sqrt{1+\sqrt{1+x}}}=\dfrac{1}{4\sqrt{1+x}}=\dfrac{1}{2\sqrt{2}}\)

\(\Leftrightarrow2\sqrt{1+x}=\sqrt{2}\Leftrightarrow1+x=\dfrac{1}{2}\Leftrightarrow x=-\dfrac{1}{2}\)

Hãy nhớ câu tính đạo hàm này, bởi nó liên quan đến nguyên hàm sau này sẽ học

Đúng(1)

NT

nguyen thi be

8 tháng 4 2021

ok cảm ơn bạn nhìu

Đúng(0)

TM

Trà Mi Liên

2 tháng 12 2015 - olm

Cho hàm số y=f(x)=2/3.x

a) Tìm f(7); f(-5/4)

b)Tìm x khi y=10

c)Tìm x khi f(x)=8

d)Vẽ đồ thị hàm số trên.

e) Hỏi điểm P(9;16) có thuộc đồ thị hàm số y=2/3 x ko?

g) Tìm điểm K và H trên đồ thị hàm số y=2/3x biết x_K =6,y_H =4.

#Toán lớp 7

0

NN

Nguyễn Ngọc Phương Linh

12 tháng 12 2016 - olm

bài 1: a/ cho hàm số \(y=\frac{3}{2}x\) . điểm E ( -4;m ) là 1 điểm thuộc đồ thị của hàm số trên. tìm m. b/ cho hàm số y=I\(m+\frac{1}{2}\)I . x-3 đi qua điểm B ( 2;-1). c/ cho hàm số y=f(x)=(2a + 3).x + . tìm a biết f(1)=-4bài 2: cho hàm số y=f(x)=\(-x^2\)+3x. tính f(-2),...

Đọc tiếp

#Toán lớp 7

0

PT

Pham Trong Bach

27 tháng 8 2017

Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1. A. k ≠ ± 2 B. k ≠ 2 C. k ≠ - 2 D. k ≠ ± 1 ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

27 tháng 8 2017

- TXĐ: D = R.

+ Với x = 1 ta có f ( 1 ) = k 2

+ Với x ≠ 1 ta có:

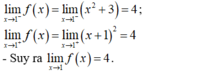
Đề kiểm tra 45 phút Đại số 11 Chương 4 có đáp án (Đề 3)

- Vậy để hàm số gián đoạn tại x = 1 khi và chỉ khi:

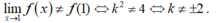
Đề kiểm tra 45 phút Đại số 11 Chương 4 có đáp án (Đề 3)

Chọn A

Đúng(0)

PT

Pham Trong Bach

29 tháng 12 2017

Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 x = 1 . Tìm k để f(x) gián đoạn tại x= 1. A. K ≢ ± 2 B. K ≢ 2 C. K ≢ - 2 D. K ≢ ± ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

29 tháng 12 2017

Đáp án A

Đúng(0)

PT

Pham Trong Bach

7 tháng 11 2019

Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1. A. k ≠ ±2. B. k ≠ 2. C. k ≠ -2....

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

7 tháng 11 2019

Chọn A.

Với x = 1 ta có f(1) = k²

Với x ≠ 1 ta có

suy ra .

Vậy để hàm số gián đoạn tại x = 1 khi ⇔ k² ≠ 4 ⇔ k ≠ ±2.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP